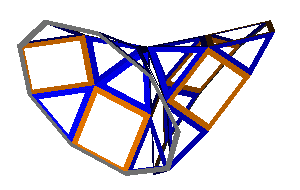
Acrohedra
The image above shows a 9-4-3 acrohedron
What is an acrohedron? An acrohedron is a polyhedron containing acrons (or vertices). Acron stems from 'acros', Greek - summit, as in Acropolis. The definition so far is not too useful. However if we define an XYZ-acron (or an 'X-Y-Z') as being a vertex surrounded in sequence by an X-gon, Y-gon and Z-gon then we can define an XYZ-acrohedron as being a polyhedron containing at least one XYZ-acron. A cube for example can be regarded as a 444-acrohedron.
Trihedral AcronsStarting with trihedral acrons, or acrons surrounded by three polygons, we can generate a list of potential acrons. To make the list manageable, we introduce two limitations:
1. We shall exclude star polygons
2. We shall only consider acrons where there is a positive angular deficit, i.e. the sum of the internal angles of the constituent polygons is less than 360 degrees.
We shall temporarily introduce a third limitation; that is for the time being we shall only consider polygons that occur in the uniform polyhedra or in the Johnson Solids. This reduces the polygons under consideration to the triangle, square, pentagon, hexagon, octagon and decagon. I have heard these polygons referred to (with tongue in cheek) as the 'polydronic' polygons after the Polydron polyhedral construction kits. Other polygons then become 'apolydronic'.
The above limitations leave a list of 34 possibilities (see table below).
For each acron we can now search for an acrohedron, specifically we can search for the minimal acrohedron. This is the polyhedron containing the requisite acron that has the minimum number of faces, edges or vertices. Interestingly not all acrons are represented in the uniform polyhedra or in the Johnson Solids. Some like the 5-4-3 have brought to light lesser-known polyhedra like the Stewart G3 or have required a specific construction, such as Professor Conway's solution for the 6-5-4. Others, like the 5-5-4, have so far eluded solution.
In certain cases the minimum acrohedron is not clear-cut. Cases such as the 5-5-5 yield a different solution (the Stewart G3) for the minimum number of vertices than for the minimum number of faces (the dodecahedron). In such cases both polyhedra are listed.
In other cases the minimum acrohedron contains flat acrons ("Flat") (eg a 6-3-3 acron) and/or coplanar faces ("Co-P") (e.g. the 6-5-4), or is self-intersecting ("S-Int") (e.g. the 10-5-3). For cases such as this all the minimal solutions are listed.
A table of dihedral angles is available here.
A list of the trihedral
acrons
follows. Note the convention that in moving from X to Y to Z, one
moves from the largest polygon to the smallest.
| Trihedral Acron |
Deficit (degrees) | V, E, F | Polyhedron |
| 3-3-3 | 180 | 4, 6, 4 | tetrahedron see also n-n-3 acrons |
| 4-3-3 | 150 | 5, 8, 5 | square pyramid (J01) |
| 4-4-3 | 120 | 6, 9, 5 | triangular prism see also n-n-3 acrons |
| 4-4-4 | 90 | 8, 12, 6 | cube |
| 5-3-3 | 132 | 6, 10, 6 | pentagonal pyramid (J02) |
| 5-4-3 | 102 | 10, 18, 9 (S-Int)
10, 20, 12 |
Small Ditrigonal Icosidodecahedron facet (self intersecting) - R.Klitzing click here for more these |
| 5-4-4 | 63 | 10, 15, 7 | pentagonal prism |
| 5-5-3 | 84 | 9, 15, 8 | tridiminished icosahedron (J63) see also n-n-3 acrons |
| 5-5-4 | 54 | none known | view some near misses |
| 5-5-5 | 36 | 13, 24,
13
20, 30, 12 |
Stewart G3 click here for more |
| 6-4-3 | 90 | 9, 15, 8 | triangular cupola (J03) |
| 6-4-4 | 60 | 12, 18, 8 | hexagonal prism |
| 6-5-3 |
72 | 28, 67, 41 (Flat, Co-P) 29, 70, 43 (Co-P) 38, 96, 60 (S-Int) |
Rayne
6-5-3 (ver 2) (flat) Rayne 6-5-3 (ver 2) (coplanar) Rayne 6-5-3 (ver 2) |
| 6-5-4 | 42 | 27,
42, 17 (S-Int)
18, 36, 20 (Co-P) 22, 48, 28 |
Rhombidodecadodecahedron facet (self intersecting) - R.Klitzing click here for more on all three |
| 6-5-5 |
24 | none known |
|
| 6-6-3 | 60 | 12, 18, 8 | truncated tetrahedron see also n-n-3 acrons |
| 6-6-4 | 30 | 24, 36, 14 | truncated octahedron |
| 6-6-5 | 12 | 21, 43, 24 (Flat, Co-P) 25, 55, 32 (Co-P) 31, 69, 40 (S-Int) |
Augmented
Q4
(flat) Augmented Q4 (co-planar) Augmented Q4 |
| 8-4-3 | 75 | 12, 20, 10 | square cupola (J04) |
| 8-4-4 | 45 | 16, 24, 10 | octagonal prism |
| 8-5-3 | 57 | none known | |
| 8-5-4 | 27 | none known | |
| 8-5-5 | 9 | none known | |
| 8-6-3 | 45 | 19, 39, 22(Flat, Co-P) 21, 46, 27 (Co-P) 27, 64, 39 (S-Int) |
Rayne
8-6-3 (ver 3) (flat) Rayne 8-6-3 (ver 3) (coplanar) Rayne 8-6-3 (ver 3) See also n-6-3 acrohedra. |
| 8-6-4 | 15 | 48, 72, 26 | truncated cuboctahedron |
| 8-8-3 | 30 | 24, 36, 14 | truncated cube see also n-n-3 acrons |
| 10-4-3 | 66 | 15, 25, 12 | pentagonal cupola (J05) |
| 10-4-4 | 36 | 20, 30, 12 | decagonal prism |
| 10-5-3 | 48 | 20, 32, 14 (S-Int)
20, 35, 17 |
icosidodecahedron facet (self-intersecting) |
| 10-5-4 | 18 | 45, 75, 32 | tridiminished rhombicosidodecahedron (J83) |
| 10-6-3 |
36 | 19, 39, 22 (Flat, Co-P) 26, 52, 28 (Co-P) 40, 70, 28 (S-Int) 30, 62, 34 |
Rayne
10-6-3 (ver 4) (flat) Rayne 10-6-3 (ver 4) (co-planar) See also n-6-3 acrohedra. Small icosicosidodecahedron facet (self intersecting) Conway 10-6-3 (non-coplanar faces) click here for more on the Klitzing and Conway polyhedra |
| 10-6-4 | 6 | 37, 78,43 (Flat, Co-P) 38, 81, 45 (Co-P) 49, 113, 66 (S-Int) 120, 180, 62 |
Rayne
10-6-4 (ver 1) (flat) Rayne 10-6-4 (ver 1) (coplanar) Rayne 10-6-4 (ver 1) (self-intersecting) truncated icosidodecahedron |
| 10-8-3 | 21 | none known | |
| 10-10-3 | 12 | 60, 90, 32 | truncated dodecahedron see also n-n-3 acrons |
Removing now our limitation to polydronic polygons, we can now consider the remaining apolydronic polygons. Acrons containing apolydronic polygons such as the heptagon also yield acrohedra. The list below shows all apolydronic trihedral acrons known to date to yield solutions. Acrons containing 7, 9 and 11-gons are listed seperately, those valid for all n (including n>=12) are then listed below. Click here for a full list of potential acrons.
| Trihedral Acron |
Deficit (Degrees) |
(V, E, F) |
Polyhedron |
| 7-4-3 | 81 3/7 | 20, 40 ,22 | 7-4-3 click here for more |
| 7-6-3 | 51 3/7 | 40,
95, 57 (Flat, Co-P) 41, 98, 59 (Co-P) 54, 136, 84 (S-Int) |
Rayne 7-6-3 ver 2 (flat) Rayne 7-6-3 ver 2 (coplanar) Rayne 7-6-3 ver 2 (self intersecting) See also n-6-3 acrohedra. |
| 7-6-4
|
21 3/7 | 27,
58, 33 (Flat, Co-P) 28, 61, 35 (Co-P) 37, 85, 50 (S-Int) |
Rayne 7-6-4T (flat) Rayne 7-6-4T (coplanar) Rayne 7-6-4S (self intersecting) See also n-6-4 acrohedra. Click here for info about another 7-6-4 acron. |
| 7-7-3 | 42 6/7 | 28, 49, 22 | Mason Green's Small Supersemicupola (self-intersecting) click here for more, see also n-n-3 acrons |
| 9-4-3 | 70 | 26, 52, 28 | 9-4-3 |
| 9-6-3 | 40 |
52,
123, 73 (Flat, Co-P) 53, 126, 75 (Co-P) 70, 176, 108 (S-Int) |
Rayne 9-6-3 ver 2 (flat) Rayne 9-6-3 ver 2 (coplanar) Rayne 9-6-3 ver 2 (self intersecting) See also n-6-3 acrohedra. |
| 9-6-4 | 10 |
35,
76, 43 (Flat, Co-P) 36, 79, 45 (Co-P) 47, 109, 64 (S-Int) |
Rayne 9-6-4T (flat) Rayne 9-6-4T (coplanar) Rayne 9-6-4S (self intersecting) See also n-6-4 acrohedra. |
| 11-4-3 | 62 8/11 | 32, 64, 34 | 11-4-3 |
| 11-6-3 | 32 8/11 | 64,
151, 89 (Flat, Co-P) 65, 154, 91 (Co-P) 86, 216, 132 (S-Int) |
Rayne
11-6-3 ver 2 (flat) Rayne 11-6-3 ver 2 (coplanar) Rayne 11-6-3 ver 2 (self intersecting) See also n-6-3 acrohedra. |
| 11-6-4 | 2 8/11 | 43,
94, 53 (Flat, Co-P) 44, 97, 55 (Co-P) 57, 133, 78 (S-Int) |
Rayne 11-6-4T (flat) Rayne 11-6-4T (coplanar) Rayne 11-6-4S (self intersecting) See also n-6-4 acrohedra. |
| 12-6-3
|
30 |
30,
63, 35 (Flat, Co-P) 36, 81, 47 (Co-P) 47, 113, 68 (S-Int) |
Rayne
12-6-3 ver 3 (flat) Rayne 12-6-3 ver 3 (coplanar) Rayne 12-6-3 ver 3 (self intersecting) See also n-6-3 acrohedra. |
| n-4-4 |
2n, 3n, n+2 |
N-gonal prism, valid for all n. |
|
| n-6-3 (n even) | 3n+2,
8n, 4n+3 (Flat, Co-P) 3n+3, 8n+3, 4n+5 (Co-P) 4n+4, 10n+8, 6n+6 (S-Int) |
Rayne n-6-3 (ver 2). See also n-6-3 acrohedra. Valid for even n>=8 (n=4 and n=6 are degenerate) Examples: n=12, n=14 |
|
| n-6-3 (n-odd) | 6n-2,14n-3,
8n+1
(Flat,
Co-P) 6n-1, 14n, 8n+3 (Co-P) 8n-2, 20n-4, 12n (S-Int) |
Rayne n-6-3 (ver 2)
See also n-6-3 acrohedra. Valid for odd n>=5 (n=3 is degenerate) Example: n=13 |
Note that the 8-6-3,
10-6-3 and 12-6-3 acrohedra are special cases where the capping
n/2-gon
of edge length 2 can be subdvided in an more efficient manner than the
generic solution. There is also a special case for the 24-6-3 but
in
this instance the subdivision of the large dodecagon requires so many
facets it is more complex than the generic case, for example the non coplanar case has
(V,E,F) = (127, 335, 210), compared to the generic
solution with (V,E,F) = (100, 248, 150).
Flat acrons, where the deficit is zero, always yield solutions. Simply join two such acrons together by a ring of squares. Click here for a full list of flat acrons.
A special case of the tri-hedral acron is the n-n-3 acron. Click here for more information on these.
Tetrahedral Acrons
Tetrahedral acrons have four surrounding polygons. In order to keep the list manageable we add to our list of restrictions as follows: the acron itself must be convex, or non-reflexive and must not be crossed. Acrons such as the crossed 4-3-4-3 occurring in the tetrahemihexahedron will not be considered here.
In considering the tetrahedral acrons we must differentiate between the X-Y-Z-Z and the X-Z-Y-Z, as the sequence of polygons is relevant.
A list of the
polydronic
tetrahedral acrons follows:
| tetrahedral acron |
Deficit (degrees) | V, E, F | Polyhedron |
| 3-3-3-3 | 120 | 5, 8, 5 | square pyramid (J01) |
| 4-3-3-3 | 90 | 8, 16, 10 | square antiprism |
| 4-3-4-3 | 60 | 8, 14, 8 | gyrobifastigium (J26) |
| 4-4-3-3 | 60 | 7, 12, 7 | elongated triangular pyramid (J07) |
| 4-4-4-3 | 30 | 12, 20, 10 | square cupola (J04) |
| 5-3-3-3 | 72 | 9, 15, 8 | tridiminished icosahedron (J63) |
| 5-3-4-3 | 42 | 14, 26, 14 | bilunabirotunda (J91) |
| 5-3-5-3 | 24 | 14, 26, 14 | bilunabirotunda (J91) |
| 5-4-3-3 | 42 | 11, 19, 10 | augmented pentagonal prism (J52) |
| 5-4-3-4 | 12 | 15, 25, 12 |
pentagonal
cupola (J05) |
| 5-4-4-3 | 12 | 20, 38, 20 | elongated bilunabirotunda |
| 5-5-3-3 | 24 | 10, 18, 10 | augmented tridiminished icosahedron (J64) |
| 6-3-3-3 | 60 | 12, 24, 14 | hexagonal antiprism |
| 6-4-4-3 | 30 | 15, 27, 14 | augmented truncated tetrahedron (J65) |
| 6-3-5-3 | 12 | 38,
81, 45
40, 87, 49 |
Conway 6-3-5-3 (coplanar faces) click here for more |
| 6-4-3-4 | 30 | 13, 22, 11 | augmented hexagonal prism (J54) |
| 6-5-3-3 | 12 | 28,
46,
20
19, 40, 23 23, 52, 31 |
Augmented Rhombidodecadodecahedron facet (self intersecting) - R.Klitzing click here for more on all three |
| 8-3-3-3 | 45 | 16, 32, 18 | octagonal antiprism |
| 8-3-4-3 | 15 | 28, 48, 22 | augmented truncated cube (J66) |
| 8-4-3-3 | 15 | 48, 116, 70 | 8-4-3-3 click here for more |
| 10-3-3-3 | 36 | 20, 40, 22 | decagonal antiprism |
| 10-3-4-3 | 6 | 65, 105, 42 | augmented truncated dodecahedron (J68) |
| 10-4-3-3 | 6 | 60, 145, 87 | 10-4-3-3 click here for more |
Removing now our limitation
to polydronic polygons, we can now consider the remaining apolydronic
polygons.
Apart from the N-3-3-3 which for all N yields the N-gonal
anti-prism (e.g. 7-3-3-3),
acrons
containing
apolydronic
polygons such as the heptagon seem to
only
rarely yield acrohedra. The list below shows all apolydronic
tetrahedral
acrons known to date to yield solutions. Click here
for a full list of potential acrons.
| Tetrahedral acron |
Deficit (degrees) | V, E, F | Polyhedron |
| 7-3-4-3 | 21 3/7 | 42, 82 ,41
44, 85, 42 |
7-3-4-3
(coplanar
faces
and
self-intersecting)
7-3-4-3 (non-coplanar faces and self-intersecting) click here for more |
Click here for flat tetrahedral acrons.
Pentahedral acrons
Turning to the
pentahedral
acrons, with the same restrictions as above, the list is short:
| Pentahedral acron |
Deficit (Degrees) | V, E, F | Polyhedron |
| 3-3-3-3-3 | 60 | 6, 10, 6 | pentagonal pyramid (J02) |
| 4-3-3-3-3 | 30 | 10, 26, 18 | sphenomegacorona (J88) |
| 5-3-3-3-3 | 12 | 30, 80, 52 | pentagonal bifrustocingulum click here for more |
No apolydronic pentahedral acrons exist as the smallest candidate, the 7-3-3-3-3, has a negative angular deficit.
Click here for flat pentahedral acrons.
Hexahedral acrons
Only one hexahedral acron exists, the 3-3-3-3-3-3. It is flat.
Credits
Many of the polyhedra referred to in this list have been identified by a search through the uniform polyhedra and the Johnson Solids. It is my expectation that a number of the minimal solutions given above will be improved upon. Some of the acrons without solutions have already generated some interesting near misses.
I am indebted to the late Professor John Conway of Princeton University for introducing me to the concept of acrohedra and for providing the list of trihedral acrons about which this page is based, Professor Conway's work is presented here with his permission. Thanks also to Melinda Green (who initiated the original search for the 5-5-4 and kicked this whole thing off) and to all contributors.
Any errors and omissions on this page are mine.
Credits for individual acrohedra are as follows:
5-4-3
Professor
John
Conway
and
Dr
Richard Klitzing
6-5-3
Rayne
H.
6-5-4
Professor John Conway and Dr
Richard Klitzing
6-6-5 Rayne H.
8-6-3
Rayne
H.
10-6-3
Professor John Conway, Alex Doskey, Dr Richard Klitzing and Rayne H.
10-6-4 Rayne H.
7-4-3 myself
7-6-3 Rayne H.
7-6-4 Rayne H.
7-7-3 Mason Green
9-4-3
myself
9-6-3 Rayne H.
9-6-4 Rayne H.
11-4-3
myself
11-6-3 Rayne H.
11-6-4 Rayne H.
n-6-3 Rayne H.
n-6-4 Rayne H.
5-4-4-3
Mick
Ayrton
6-3-5-3
Professor John Conway
6-5-3-3 Alex Doskey
7-3-4-3 myself
8-4-3-3
myself
10-4-3-3
myself
5-3-3-3-3
Janella
Large
and
Mick
Ayrton