n-6-3 acrohedra
Rayne
H. has in 2023 discovered a very elegant and infinite family of n-6-3
acrohedra. The construction varies slightly between even and odd
values of n. Rayne's explanation of their construction is here.
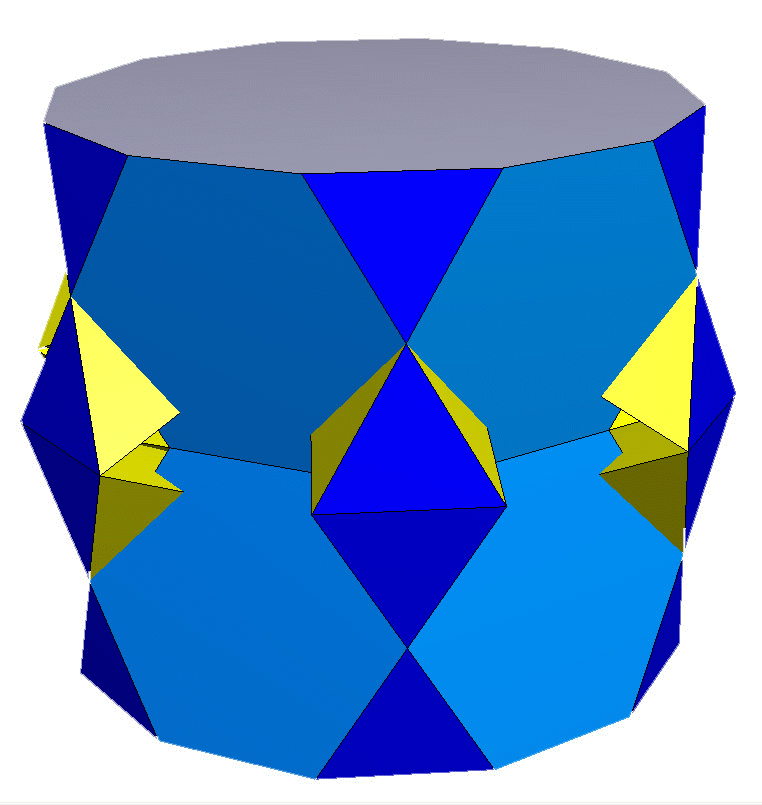
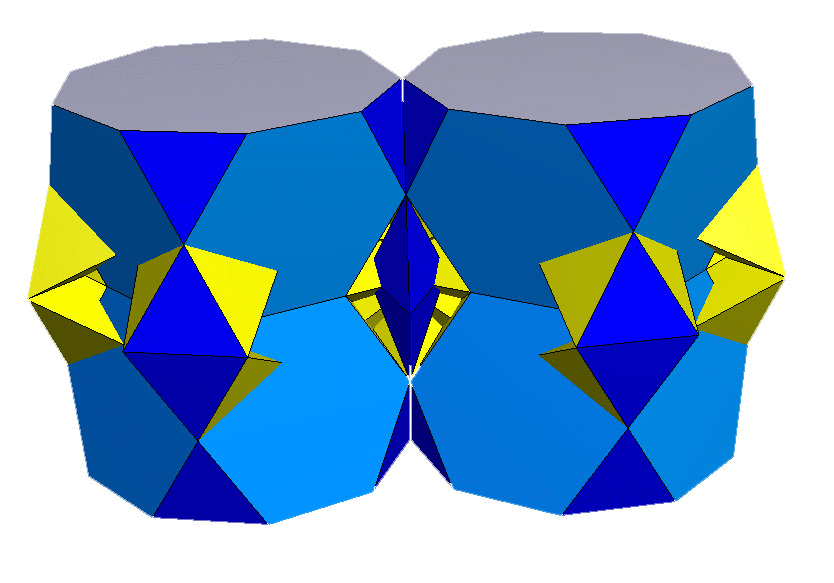
The above construction includes coplanar faces. These can be
resolved
by the excavation of tetrahedra from the coplanar triangles to form
figures such as those above.
Figures can be generated for n=5 and all n>=7.
Models with n=3, n=4 and n=6 are degenerate.
Figures for n = 5 7
8 9 10 11 12 13 14 16 18
Whilst containing n-6-3 acrons, these figures are not the minimal
acrohedra for any value of n.
Back: to
acrohedra
