
One cycle: Tetrahedron
n-n-3 acrohedra


Mason Green's discovery (October 2005) of a 7-7-3 acrohedron has sparked interest in the polyhedra that can be formed with n-n-3 acrons for varying values of n.
The rules followed in generating the 7-7-3 acrohedron can be generalised as follows, these could be termed 'Green's Rules':
1. Take an n-gonal polygon
2. Attach both an n-gon and a triangle to each edge of this polygon
3. Remove the original polygon
4. Connect the open edges of each triangle to the first open edges of the n-gons
5. Attach the next open edge of each n-gon to the neighbouring n-gon.
6. Attach the next open edge of each n-gon to a new layer of triangles.
7. Repeat the process from step 4, or close the polyhedron as appropriate.
Absolute values for which n-n-3 acrons exist are for 12/5 < n < 12. At the limits the acrons become planar. Values within this range for which acrons are known are given below. For even values of n (and n=3), a simpler acrohedron can simply be formed by cycling a base n-gon with alternate n-gons and triangles and then finding suitable polygons (for n>5) to close up the top. For odd values of n, the base polygon must be circled twice (as is effectively described above). In order to obtain similar figures for even and odd n, the above process has been followed for even n even though it is not necessary to form an acron. The result in these cases are gyrated blend models.
Incidence matrices are provided courtesy of Dr Richard Klitzing.
3-3-3
| Green's Rules: degenerate. |  One cycle: Tetrahedron |
3 * | 2 2 | 4
* 1 | 0 6 | 6
----+-----+--
2 0 | 3 0 | 2
1 1 | 0 6 | 2 pairwise co-incident
----+-----+--
2 1 | 1 2 | 6 pairwise co-incident
4-4-3
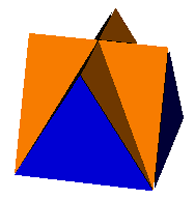 Green's Rules: Gyrated blend of digonal cupolae. |
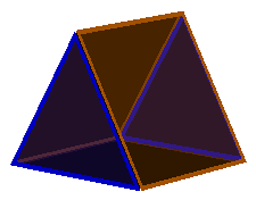 One cycle: Digonal cupola (triangular prism) |
4 * | 2 2 0 | 2 2
* 4 | 0 2 1 | 2 1
----+-------+----
2 0 | 4 * * | 1 1
1 1 | * 8 * | 1 1
0 2 | * * 2 | 2 0
----+-------+----
2 2 | 1 2 1 | 4 *
2 1 | 1 2 0 | * 4
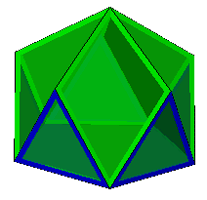
5-5-3

Green's Rules: Icosahedron facet
5 * * | 2 2 0 | 2 2
* 5 * | 0 2 1 | 2 1
* * 1 | 0 0 5 | 5 0
------+--------+----
2 0 0 | 5 * * | 1 1
1 1 0 | * 10 * | 1 1
0 1 1 | * * 5 | 2 0
------+--------+----
2 2 1 | 1 2 2 | 5 * {5/1} resp. {5/2}
2 1 0 | 1 2 0 | * 5
6-6-3
 Green's Rules: Gyrated blend of truncated tetrahedra. |
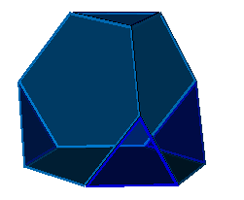 One cycle: Truncated tetrahedron |
6 * * | 2 2 0 0 | 2 2 0
* 6 * | 0 2 1 0 | 2 1 0
* * 6 | 0 0 1 2 | 2 0 1
------+----------+------
2 0 0 | 6 * * * | 1 1 0
1 1 0 | * 12 * * | 1 1 0
0 1 1 | * * 6 * | 2 0 0
0 0 2 | * * * 6 | 1 0 1
------+----------+------
2 2 2 | 1 2 2 1 | 6 * *
2 1 0 | 1 2 0 0 | * 6 *
0 0 3 | 0 0 0 3 | * * 2
7-7-3

Green's Rules Mason Green's supersemicupola
7 * * * | 2 2 0 0 0 | 2 2 0 0
* 7 * * | 0 2 1 0 0 | 2 1 0 0
* * 7 * | 0 0 1 2 0 | 2 0 1 0
* * * 7 | 0 0 0 2 2 | 1 0 2 1
--------+-------------+--------
2 0 0 0 | 7 * * * * | 1 1 0 0
1 1 0 0 | * 14 * * * | 1 1 0 0
0 1 1 0 | * * 7 * * | 2 0 0 0
0 0 1 1 | * * * 14 * | 1 0 1 0
0 0 0 2 | * * * * 7 | 0 0 1 1
--------+-------------+--------
2 2 2 1 | 1 2 2 2 0 | 7 * * * {7/1} resp. {7/2}
2 1 0 0 | 1 2 0 0 0 | * 7 * *
0 0 1 2 | 0 0 0 2 1 | * * 7 *
0 0 0 7 | 0 0 0 0 7 | * * * 1 {7/2} resp. {7/3}
8-8-3
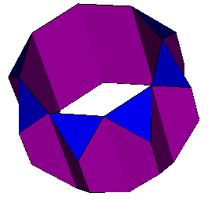 Two cycles: Gyrated blend of truncated cubes. |
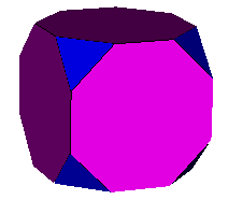 One cycle: Truncated cube |
blend of 2 truncated cubes
{8/3} 2 stellated truncated hexahedra
8 * * * | 2 2 0 0 0 | 2 2 0
* 8 * * | 0 2 1 0 0 | 2 1 0
* * 8 * | 0 0 1 2 0 | 2 0 1
* * * 8 | 0 0 0 2 2 | 2 0 2
--------+-------------+------
2 0 0 0 | 8 * * * * | 1 1 0
1 1 0 0 | * 16 * * * | 1 1 0
0 1 1 0 | * * 8 * * | 2 0 0
0 0 1 1 | * * * 16 * | 1 0 1
0 0 0 2 | * * * * 8 | 1 0 1
--------+-------------+------
2 2 2 2 | 1 2 2 2 1 | 8 * * {8/1} resp. {8/3}
2 1 0 0 | 1 2 0 0 0 | * 8 *
0 0 1 2 | 0 0 0 2 1 | * * 8
or with additional top-down symmetry
16 * | 2 2 0 | 2 2
* 16 | 0 2 1 | 2 1
------+---------+-----
2 0 | 16 * * | 1 1
1 1 | * 32 * | 1 1
0 2 | * * 8 | 2 0
------+---------+-----
4 4 | 2 4 2 | 8 * {8/1} resp. {8/3}
2 1 | 1 2 0 | * 16
9-9-3
no solution known
10-10-3
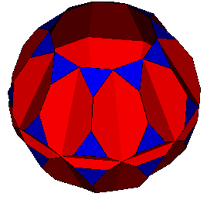 Green's Rules: Gyrated blend of truncated dodecahedra |
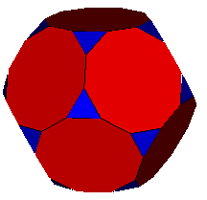 One cycle: Truncated dodecahedron |
blend of 2 truncated dodecahedra
{10/3} 2 great stellated truncated dodecahedra
10 * * * *
* *
* | 2 2 0 0 0 0 0
0 0
0 0 | 2 2 0 0 0 0
* 10 * * * * * * |
0 2
1 0 0 0 0 0 0 0 0
| 2
1 0 0 0 0
* * 10 * * * * * |
0 0
1 2 0 0 0 0 0 0 0
| 2
0 1 0 0 0
* * * 20 * * * * |
0 0
0 1 1 1 0 0 0 0 0
| 1
0 1 1 0 0
* * * * 20 * * * |
0 0
0 0 0 1 1 1 0 0 0
| 1
0 0 1 1 0
* * * * * 10 * * |
0 0
0 0 0 0 0 2 1 0 0
| 0
0 0 2 1 0
* * * * * * 10 * |
0 0
0 0 0 0 0 0 1 2 0
| 0
0 0 2 0 1
* * * * * * * 10 |
0 0
0 0 0 0 0 0 0 2 2
| 0
0 0 2 0 2
------------------------+----------------------------------+------------------
2 0 0 0 0 0 0 0 |
10 *
* * * * * * * * *
| 1
1 0 0 0 0
1 1 0 0 0 0 0 0 |
* 20
* * * * * * * * *
| 1
1 0 0 0 0
0 1 1 0 0 0 0 0 |
*
* 10 * * * * * * * *
| 2
0 0 0 0 0
0 0 1 1 0 0 0 0 |
*
* * 20 * * * * * * *
| 1
0 1 0 0 0
0 0 0 2 0 0 0 0 |
*
* * * 10 * * * * * *
| 0
0 1 1 0 0
0 0 0 1 1 0 0 0 |
*
* * * * 20 * * * * *
| 1
0 0 1 0 0
0 0 0 0 2 0 0 0 |
*
* * * * * 10 * * * *
| 1
0 0 0 1 0
0 0 0 0 1 1 0 0 |
*
* * * * * * 20 * * *
| 0
0 0 1 1 0
0 0 0 0 0 1 1 0 |
*
* * * * * * * 10 * *
| 0
0 0 2 0 0
0 0 0 0 0 0 1 1 |
*
* * * * * * * * 20 *
| 0
0 0 1 0 1
0 0 0 0 0 0 0 2 |
*
* * * * * * * * * 10
| 0
0 0 1 0 1
------------------------+----------------------------------+------------------
2 2 2 2 2 0 0 0 |
1
2 2 2 0 2 1 0 0 0
0 | 10
* * * * *
2 1 0 0 0 0 0 0 |
1
2 0 0 0 0 0 0 0 0
0 |
* 10 * * * *
0 0 1 2 0 0 0 0 |
0
0 0 2 1 0 0 0 0 0
0 |
* * 10 * * *
0 0 0 2 2 2 2 2 |
0
0 0 0 1 2 0 2 2 2
1 |
* * * 10 * *
0 0 0 0 2 1 0 0 |
0
0 0 0 0 0 1 2 0 0
0 |
* * * * 10 *
0 0 0 0 0 0 1 2 |
0
0 0 0 0 0 0 0 0 2
1 |
* * * * * 10
or given with additional top-down symmetry
20 * * * | 2
2 0
0 0 0 | 2 2 0
* 20 * * | 0 2 1 0
0 0 |
2 1 0
* * 20 * | 0 0 1 2
0 0 |
2 0 1
* * * 40 | 0 0 0 1
1 1 |
2 0 1
------------+-------------------+---------
2 0 0 0 | 20 * * *
* * |
1 1 0
1 1 0 0 | * 40 * *
* * |
1 1 0
0 1 1 0 | * * 20 *
* * |
2 0 0
0 0 1 1 | * * * 40
* * |
1 0 1
0 0 0 2 | * * * *
20 * |
1 0 1
0 0 0 2 | * * * *
* 20 |
2 0 0
------------+-------------------+---------
2 2 2 4 | 1 2 2 2
1
2 | 20 * * {10/1} resp. {10/3}
2 1 0 0 | 1 2 0 0
0
0 | * 20 *
0 0 1 2 | 0 0 0 2
1
0 | * * 20
11-11-3
no solution known
Solutions containing star polygons.
With the absolute range of 12/5 < n < 12, solutions can also be found for the star polygons given below. The rules followed are the same as those above, the resulting figures are isomorphs of the above solutions. Incidence matrices are as above.
5/2-5/2-3
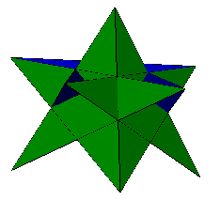
Green's Rules: Great icosahedron facet
7/2-7/2-3
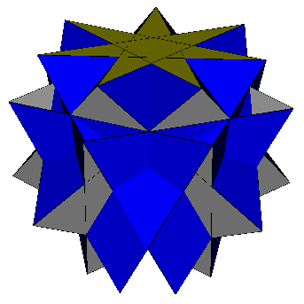
Green's Rules: Mason Green's great supersemicupola
8/3-8/3-3
 Green's Rules: Gyrated blend of stellated truncated hexahedra |
 One cycle: Stellated truncated hexahedron |
10/3-10/3-3
 Two cycles: Gyrated blend of great stellated truncated dodecahedra |
 One cycle: Great stellated truncated dodecahedron |