


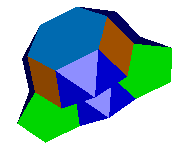
The minimal non-self-intersecting case can be improved upon if we permit self-intersection. Dr Richard Klitzing has studied the facets of the small icosicosidodecahedron amongst which was the above 28-faced figure, this is one of a number of 28-faced facets. It is chosen as it is the facet with the fewest vertices and edges. Dr Klitzing informs me that he has to date only studied facets with a three-fold or five-fold symmetry, so this result may still be improved upon.
The full results of Dr Klitzing's work on faceting a number of the uniform polyhedra are hosted by Ulrich Mikloweit here.
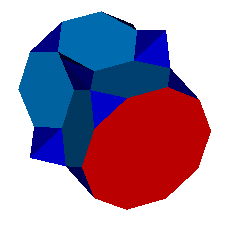
The Doskey triacontadecadihedron
imaged above
was discovered by Alex Doskey [Alex@Doskey.com],
while it is not a minimal solution it is notable for an unusual degree
of symmetry not anticipated in the solution for an acron not found amongst
the uniform polyhedra or the Johnson
Solids.
6-3-5-3

Professor Conway's solution
to the 10-6-3 acrohedron also forms the basis for resolving the 6-3-5-3
acrohedron.
The 10-6-3 acrohedron is 'augmented' by replacing the decagonal face with
a pentagonal rotunda. The rotunda is placed
such that the triangles appended to the decagons are offset from each other.
Again the coplanar faces can be resolved by the addition of two tetrahedra to
form this solution.
With the rotunda gyrated such that the triangular faces are joined by an edge, the two triangles forming the 6-5-3-3 acron are coplanar. A polyhedron containing a convex 6-5-3-3 acron has though been discovered based on Professor Conway's solution to the 6-5-4 acron.