In addition to the successes in finding new polyhedra to fill the gaps in the table of minimal acrohedra, there have also been some notable near misses.  Some of which are presented here.  

These polyhedra are also presented as 'Stress Maps', a bespoke form of VRML model for showing distortion in such models.  More information on Stress Maps and distortion is available here.

(E=0.00302, P=0, A=0.56º)	(E=0.00159, P=0, A=0.29º)	(E=0.00062, P=0, A=0.11º)
stress map  (cones exaggerated x 200)	stress map  (cones exaggerated x 200)	stress map  (cones exaggerated x 500)

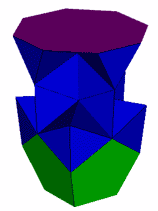
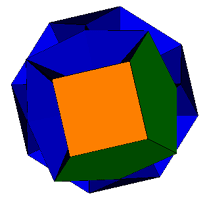
This discovery of mine is a very close near miss to a polyhedron with a 5-5-4 vertex.  All faces except the triangles are regular.  Some of the triangles are slightly distorted.  The original figure is to the left, the figure in the centre has four square faces augmented to reduce the distortion (the augmentation was inspired by Mick Ayrton's near miss below), the figure on the right has two of the four pentagons augmented (inwards) to further reduce the distortion, this figure is the closest discovery to date to a 5-5-4 acrohedron.  It is curious that the lowest distortion in the centre case has the square pyramids pointing outwards, whereas in the right hand case, the lowest distortion is achieved with the pentagonal pyramids and the square pyramids both pointing inwards.

(E=0.00436, P=0, A=0.78º)	(E=0.00193, P=0, A=0.36º)
stress map  (cones exaggerated x 200)	stress map  (cones exaggerated x 200)

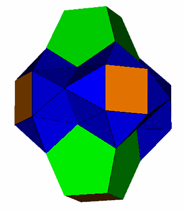
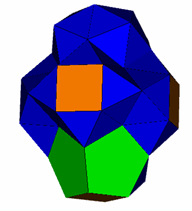
This discovery of Mick Ayrton's is another tantalisingly close near miss.  All faces except the triangles are regular.  Some of the triangles are slightly distorted.  The original figure is to the left, the figure on the right has six of the eight pentagonal faces augmented to reduce the distortion. (Augmenting the lateral square faces has no significant effect.

This 5-5-4 near miss was discovered by Melinda Green and modelled by Alex Doskey.  All faces are distorted. (stress map).  
(cones exaggerated x 10)  Distortion: (E=0.028, P=0.718,A=24.4º)

This 5-5-4 near miss was discovered and modelled by Alex Doskey.  Only the triangular faces are distorted. (stress map).  Distortion: (E=0.248, P=0, A=46º)

This 5-5-4 near miss above was discovered by Professor John Conway and modelled by myself.  Only the triangular faces are distorted. (stress map).  Distortion: (E=0.126, P=0, A=22.1º)

This 5-5-4 near miss was discovered by myself in 2005.  It was an attempt to solve the 5-5-4 acron by following Mason Green's methodology by which the 7-7-3 acron was solved.  The distortion is restricted to the triangular faces.  (Stress map).  Distortion: (E=0.517, P=0, A=88.5º)

The above 5-5-4 near miss is the 'associahedron'.  All faces are distorted. (Stress map)   Distortion: (E=0.097, P=2.779, A=47.9°).  Thanks to Roger Kaufman for bring this near miss to my attention.

The name derives from the fact that there are 14 ways to bracket 5 numbers.  Each vertex of the associahedron corresponds to one particular bracketing.  An edge exists between two vertices if the two bracketing patterns that correspond to these two vertices differ by only one set of brackets.  More information can be found at:
http://www.cs.bsu.edu/homepages/fischer/math215/associahedron.html and 
http://www.ac-noumea.nc/maths/amc/polyhedr/3D-img_.htm

Back: to near-miss index
Back: to site index