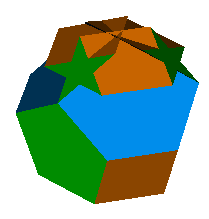
The minimal 6-5-4 acrohedron (20 faces) imaged above left was discovered by Professor John Conway.  It was the result of a specific search for a solution for the 6-5-4 acron.   It is notable in that it contains a number of coplanar faces.  These can be removed by the addition of four additional tetrahedra.  The result is imaged above right (28 faces).  For the semi-hexagonal faces, the tetrahedra must face inwards to avoid further coplanarity problems.  Note, the coplanar figure is mentioned in passing in Professor Bonnie Stewart's "Adventures Among the Toroids" (2nd Edition page 168), where it receives the name W'.  In this case it is a transitional phase in the generation of a triangular hebesphenorotunda from a tri-diminished icosahedron.  

The minimal non-coplanar case can be improved upon if we permit self-intersection. Dr Richard Klitzing has studied the facets of the rhombidodecadodecahedron, amongst which was the above 17-faced figure.  Dr Klitzing informs me that he has to date only studied facets with a three-fold or five-fold symmetry, so this result may still be improved upon.  (Note, the previous example of a 21-faced polyhedron with five-fold symmetry is linked here)

The full results of Dr Klitzing's work on faceting a number of the uniform polyhedra are hosted by Ulrich Mikloweit here.

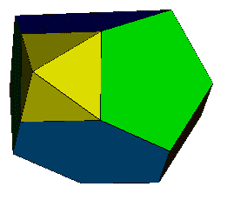
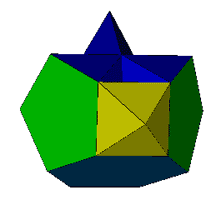
The minimal 6-5-3-3 acrohedron (23 faces) imaged above left was discovered in 2005 by Alex Doskey, it is formed by augmenting one of the square faces in Professor John Conway's 6-5-4 acrohedron with a  square pyramid.  It does though retain the coplanar faces of the original figure.  These can be removed by the addition of four additional tetrahedra.  The result is imaged above right (31 faces).  For the semi-hexagonal faces, the tetrahedra must face inwards to avoid further coplanarity problems.  In both cases the augmented faces are highlighted.

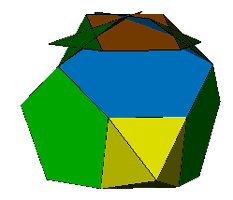
Again the minimal non-coplanar case can be improved upon if we permit self-intersection.  If we perform a similar augmentation to Dr Richard Klitzing's rhombidodecadodecahedron facet, we can obtain the above 20-faced figure.  The augmented faces are highlighted.

Back: to acrohedra