Near Misses
Jump to newest entry.
Johnson Solid Near Misses
When Norman Johnson was cataloging the convex polyhedra in the 1960's, he apparently came across "a number of tantalisingly close misses". A selection of such polyhedra are shown below:
A 'near-miss' polyhedron is one in which the faces are not quite regular. In many cases physical models can be made without any apparent distortion or 'forcing' of the faces. The 'nearness' of a miss is the subject of some debate amongst polyhedronists. No good definition exists. My own quantification (which I admit has its faults) is to define a triplet of figures:
'E' is the sum of the distortions of all of the edge lengths (assuming an edge length of 1)
'P' is the polygonal distortion, it is expressed as the sum of the distortion of all of the diagonals across each polygon. For polygons other than triangles, forms exist with all edge lengths 1 which are not regular (eg a rhombus).
'A' is the aggregate angular error. The absolute difference is determined between the angle of a regular polygon and the angle in the modelled polygon. These are summed for each angle in each polygon.
There are two ways in which these numbers can be read. 'E' and 'P' are both measures of side distortion ('E' is edges; 'P' is diagonals), there is an element of trade off between the two. An approximation to the extent of the distortion is given by 'E+P'. The accepted practice is that the distortion is confined to the smallest faces.
'A' is a standalone measure of distortion, and is an attempt to quantify the 'nearness' of a near-miss in a single value. This has its shortcomings though as (for example) a rectangular face would give an 'A' value of zero.
Presented are below are the closest Johnson Solid near misses ranked according to the parameter 'A'. Unless numbers get out of hand, I will extend this list to include any polyhedron meeting the criteria below with a value of A < 60°
To qualify as a Johnson Solid near miss (for the purposes of this list), a polyhedron must meet the following criteria:
Further submissions are welcome.
Number 1: A=5.1°
This augmented pentagonal prism was discovered by Alex Doskey in 2006. It can be formed by taking a pentagonal prism and augmenting two adjacent square faces with pyramids. Then augment the two adjacent triangular faces that result with tetrahedra. The result can be seen here. Note the two 'peaks' of the tetrahedra almost co-incide and there are a number of coplanar triangles. If a model is formed with these vertices together a convex figure results, the coplanar triangles in the original figure now have a dihedral angle 179.665º. (Stress map). Distortion (E=0.027, P=0 , A=5.07°). A convex variation can be formed where the opposite square face of the pentagonal prism is also augmented with a pyramid, the distortion statistics are the same.
Number 2: A=7.6° New Entry 08 Mar 10
This near miss was discovered by Bill Myers in March 2010. Only the triangular faces are distorted. (Stress map). Distortion: (E=0.045, P=0, A=7.6º). The pair of triangles which look almost coplanar have a dihedral angle of 177.3º.
Number 3: A=10.9°
This near miss was discovered by Roger Kaufman in 2006. Only the triangular faces are distorted. (Stress map). Distortion: (E=0.059, P=0, A=10.9º). It can be formed by augmenting an augmented triangular prism (J49) with two pyramids (one on a square face and one on an adjacent face on the original augmentation) and then 'filling' the gap with a tetrahedron.
Number 4: A=18.3°
This trisquare hexadecatrihedron has 16 triangular and 3 square faces, and looks somewhat like a cube embedded in an icosahedron (hence my informal name of 'cubicos'), . The squares are regular and the aggregate distortion in the lengths of the triangular edges is only about 0.1 in total (stress map). Distortion (E=0.10, P=0 , A=18.3°).
Number 5: A=24.0°
This near miss, discovered by Roger Kaufman in 2006, resembles the Johnson Solid 'bilunabirotunda' with one of the 'rotundas' replaced by a chain of three square faces. The pentagons are regular and the distortion is confined to the squares and the triangles. (stress map). Distortion (E=0.134, P=.300 , A=24.0°).
This near miss containing a 5-5-4 acron was discovered by Melinda Green and modelled by Alex Doskey. The triangular and square faces are distorted, but the pentagonal faces are regular. (Stress map). Distortion: (E=0.028, P=0.718,A=24.4º). Note: the pentagons can be augmented resulting in further figures, some of which can be formed with regular squares and triangles. Such examples are listed separately below.
Number 7: A=34.0°
A family of 'wedges' can be obtained by attaching an n-gon to an (n+1)-gon by one square and a ring of triangles. Above the {3}-(4} wedge the wedges cease to be regular and exhibit gradually higher levels of distortion. This distortion can always be confined to the triangular faces and is most apparent for the faces close to the square face. For the {4}-(5} wedge, the triangle-triangle edges are distorted by 0.19 (stress map), Distortion (E=0.194, P=0 , A=34.0°).
Roger Kaufman has pointed out to me that either of the square faces in this polyhedron can be augmented with a square pyramid to form distinct Johnson Solid Near Misses. As the square face that is being augmented is regular, the augmentation does not affect the distortion statistics. Top square augmented (stress map). Side square augmented (stress map)
Number 8: A=34.7° New Entry 24 Jan 10
This near miss based on the Snub Antiprism was discovered by Roger Kaufman. It is generated in similar fashion to his other J85 based discoveries but In this case, it involves part of a pentagonal prism fitting into a space made on one side. Only the triangular faces are distorted. (Stress map) Distortion: (E=0.185, P=0, A=34.7º).
Number 9: A=35.4°
This near miss was discovered by Mick Ayrton in 2006. The distortion is confined to the triangles. (stress map) Distortion: (E=0.134, P=0, A=35º). If the condition that the distortion is confines to the smallest faces is relaxed such that all faces are allowed to distort (here, stress map) then the distortion becomes (E=0.0212, P=0.017, A=6.5º), a value of A that would claim a much higher position.
This near miss based on the Snub Antiprism was discovered by Roger Kaufman in November 2009. In Roger's words: "Take the Snub Antiprism J85 and remove one square and two opposite adjoining triangles to the square. What is left is now flexible. Flex it until the triangular gaps are 90 degrees and insert 2 squares. Now there will be two triangular holes left and fill those in." Only the triangular faces are distorted. (Stress map) Distortion: (E=0.191, P=0, A=40.2º). See also the associated model with both squares of the Snub Antiprism replaced.
Number 11: A=42.1° New Entry 06 Mar 10
This near miss was discovered by Bill Myers in March 2010. Only the triangular faces are distorted. (Stress map) Distortion: (E=0.192, P=0, A=42.1º). The pair of triangles which look almost coplanar have a dihedral angle of 177.5º.
Number 12: A=43.1°
This near miss containing a 6-5-4 acron was discovered by Alex Doskey in 2006. Only the triangular and square faces are distorted. (Stress map) Distortion: (E=0.0387, P=0.535, A=43º).
This near miss containing a 6-5-5 acron was discovered by Robert Webb. Only the triangular faces are distorted. (Stress map) Distortion: (E=0.170, P=0, A=44.7º).
Number 14: A=45.3°
This near miss was discovered by myself in 1999 (unnamed) and re-discovered independently by Roger Kaufman in 2006, Roger calls it an hexagonal 'square barrel'. The distortion is confined to the triangular and square faces (stress map). Distortion: (E=0.029, P=1.36, A=45º).
This polyhedron is a member of a family of polyhedra where for one particular value of n/d the polyhedron would be regular. Roger and Adrian Rossiter have calculated that this value is:
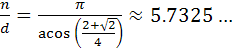
Values of n/d between 5 and 6 which have been tested are as follows:
n/d = 5 (stress map). Distortion: (E=0.064, P=3.88, A=87º).
n/d = 11/2 (5.5) (stress map). Distortion: (E=0.042, P=2.42, A=67º).
n/d = 40/7 (5.714...) Distortion: (E=0.013, P=0.66, A=20º).
n/d = 23/4 (5.75) Distortion: (E=0.007, P=0,36, A=11º).
n/d = 6 (stress map). Distortion: (E=0.029, P=1.36, A=45º)
n/d = 23/4 shows the minimal value of A to date for this family, although it should be noted that non integer values of n/d are not near miss Johnson Solids as they are not convex polyhedra. Further (un-modelled) values of n/d which should give low values for A are: 63/11, 86/15, 103/18, 109/19, 149/26 ... but by this point the star polygon is too complex to model. For a really close value (to Roger's prediction) try 9109/1589. Alex Doskey has also pointed out that 3365/587 and 2872/501 should give the best values for d<1000.
It is interesting to note the almost
linear
relationship between E (and to a lesser extent A) and
the product
of the error from Roger's value and d (i.e. the number of loops around
the
symmetry axis.

Roger Kaufman has also (in 2013)
discovered a 'great square barrel' by changing the sign in the above
equation
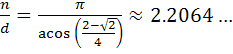
The above image shows the n/d=11/5 example - this is an isomorph to
the n/d =
11/2 square barrel.
Number 15: A=45.7°
This near miss containing dodecagons was discovered by Roger Kaufman in 2006. It is an expanded version of Robert Webb's 6-5-5 acron shown above. Only the triangular and square faces are distorted. It is the closest near miss discovered to date to contain an 'apolydronic' polygon. (Stress map) Distortion: (E=0.369, P=1.07, A=45.7º).
This near miss based on the Snub Antiprism was discovered by Roger Kaufman in November 2009. Proceed as per the associated model with one square of the Snub Antiprism replaced, then repeat the process for the other square. Only the triangular faces are distorted. (Stress map) Distortion: (E=0.217, P=0, A=46.7º).
This near miss was discovered independently by both Robert Webb and Alex Doskey in 2002. Only the triangular faces are distorted. (Stress map) Distortion: (E=0.263, P=0, A=47.7º). See also an augmented form.
Number 18: A=48.5°:
This near miss was discovered by Roger Kaufman in 2006. Only the triangular faces are distorted. (Stress map) Distortion: (E=0.245, P=0, A=48.5º). Roger discovered this figure by 'knocking parts off a sphenomegacorona' but it can as Roger also points out be made by augmenting a gyrobifastigium.
Number 19: A=50.8° New Entry 12 Mar 10
This near miss was discovered by Bill Myers in March 2010. Only the triangular faces are distorted. (Stress map). Distortion: (E=0.282, P=0, A=50.8º). It can be regarded as an augmented form of this polyhedron.
Number 20: A=50.9°
This near miss was discovered by Roger Kaufman in 2006. Only the triangular faces are distorted. (Stress map) Distortion: (E=0.234, P=0, A=51º).
In Roger's words: "I found this while messing around with Stewart X. But it can also be derived by cutting J91 in half. Do a self augmentation of that half. Then there is a non-convex part. By augmenting pyramids on that it came close to closing. It can then be faceted and sprung into shape such that only those triangles are distorted."
Number 21: A=52.1° New Entry 3 Jan 2010
The above polyhedron was discovered by Ulrich Mikloweit in 2009, there is also a variation with a pentagonal pyramid removed. Only the triangular faces are distorted. (Stress map) Distortion: (E=0.273, P=0 , A=52.1°)
Number 22: A=52.47°
The above polyhedron is an example of a 'fullerene', and was brought to my attention by Robert Austin and Roger Kaufman. It has tetrahedral symmetry with 12 pentagons and 4 hexagons and as such is the closest near miss with higher than prismatic symmetry. The above model has the distortion confined to the pentagons, stress map. Distortion (E=0.316, P=3.07 , A=52.47°). If the hexagons are allowed to distort (here, stress map) then the distortion becomes (E=0.059, P=2.19 , A=108°)
Number 23: A=52.50°
This near miss was discovered by Roger Kaufman in 2007. It is an augmented form of Melinda Green's 5-5-4 acron. All four pentagonal faces are replaced with pentagonal pyramids. This allows the distortion to be confined to the triangular faces, with the square faces remaining regular. (Stress map). Distortion: (E=0.264, P=0, A=52.50º).
Number 24: A=53.6° New Entry 09 Mar 10
This near miss was discovered by Bill Myers in March 2010. Only the triangular faces are distorted. (Stress map). Distortion: (E=0.274, P=0, A=53.6º).
Number 25: A=54.0°
A short personal diversion here: This 'potato' is the first near miss I came across, I was actually attempting to model a disphenocingulum from Polydron and I inadvertently rotated one of the sphenoid caps by one edge length with respect to the other. Having then discovered I had not it in fact generated a disphenocingulum, I contacted George Hart to ask what it was. George kindly did some research of his own (including correspondence with Norman Johnson) and replied telling me it was a 'near-miss', he also offered to host a model of this on his website should I manage to generate one. Three months later I had succeeded, and the first (quick-basic form of) HEDRON was born. I term it a 'quasi-gyro-disphenocingulum'. All of the distortion in the linked model is contained in the triangular faces (stress map). Distortion (E=0.261, P=0, A=54.0°). If the triangular faces are forced to be regular, the square faces become rhombi with acute angles of just over 79 degrees (here).
Number 26: A=54.1°
This near miss was discovered by Roger Kaufman in 2007. It is an augmented form of Melinda Green's 5-5-4 acron. Two pentagonal faces are replaced with pentagonal pyramids. This allows the distortion to be confined to the triangular faces, with the square faces remaining regular. (Stress map). Distortion: (E=0.243, P=0, A=54.1º). Note: augmenting only one of the pentagons, or two vertex adjacent pentagons results in a figure which requires the triangles and the squares to be distorted, such figures can be regarded as Melinda Green's 5-5-4 acron with a regular pentagon augmented and so are not seperately listed. A further version has three pentagons augmented but has the same distortion as this figure and so can be regarded as an augmentation.
Number 27 A=54.7° New Entry 3 Jan 2010
The above polyhedron was discovered by Ulrich Mikloweit in 2009, there is also a variation with the pentagon replaced by a pentagonal pyramid. Only the triangular faces are distorted. (Stress map) Distortion: (E=0.265, P=0 , A=52.1°)
Number 28: A=54.9° New Entry 29 April 2010
This near miss was discovered by Bill Myers in April 2010. Only the triangular faces are distorted. (Stress map). Distortion: (E=0.304, P=0, A=54.9º).
Number 29: A=56.0°
This near miss was discovered by Ulrich Mikloweit in 2007. Only the triangular faces are distorted. (Stress map) Distortion: (E=0.208, P=0, A=56.0°)
Number 30: A=56.4°
This discovery of Mick Ayrton's (which he terms a 'saucer') contains two caps from the Johnson Solid 'trigyrate rhombicosidodecahedron'. Stress map. Distortion (E=0.214, P=0, A=56.4°). Interestingly, if the pentagons are replaced by pentagonal pyramids (here), the model becomes regular. Mick has pointed out that this occurs to a surprising number of near misses.
Number 31: A=57.6°
This near miss was discovered by Roger Kaufman in 2007. It can be considered a truncated form of the disphenocingulum. The distortion is confined to the triangular faces. (Stress map). Distortion: (E=0.318, P=0, A=57.6º).
This
Near Miss candidate was discovered by Ulrich Mikloweit in 2025.
The model linked below has the distortion limited to the
triangle-triangle edges. Unfortunately it does not qualify for
the list as it has an Angular
Distortion of some 148º.