
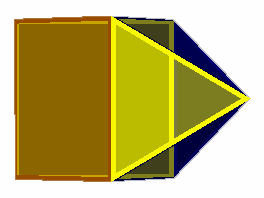
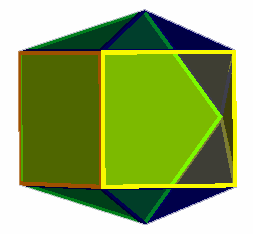

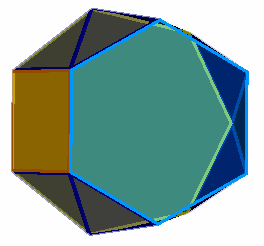
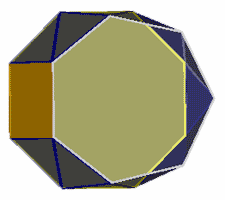
A family of 'wedges' (images above) can be obtained by attaching an n-gon to an (n+1)-gon by one square and a ring of triangles. The {2}-(3} wedge is more commonly described as a square pyramid. The {3}-{4) wedge is also regular and is found amongst the Johnson Solids as the augmented triangular prism. Beyond this point, the wedges cease to be regular and exhibit gradually higher levels of distortion. This distortion can always be confined to the triangular faces and is most apparent for the faces close to the square face. For the {4}-(5} wedge, the triangle-triangle edges are distorted by 0.192 (stress map), the {5}-{6} wedge has a distortion of 0.363 (stress map), the {6}-(7) wedge a distortion of 0.54 (stress map) and the {7}-{8} wedge a distortion of 0.669 (stress map). Further members of this family have not been explored.
Returning to the {4}-(5} wedge, it is interesting to note that if the square and pentagonal bases are augmented with pyramids, then a regular solid can be obtained. This is the Johnson Solid 'augmented sphenocorona', shown here with the pyramids highlighted. Roger Kaufman has also pointed out to me that a regular (but non-convex) figure can be generated by augmenting the {5}-{6} wedge.
Distortion:
{4}-(5} wedge (E=0.19, P=0 , A=34°)
{5}-{6}
wedge (E=0.36, P=0 , A=71°)
{6}-(7)
wedge (E=0.54, P=0 , A=109°)
{7}-{8} wedge
(E=0.67, P=0 , A=143°)