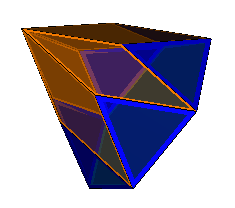
Molybi Augmented Polyhedra
In this page I discuss a simple class of polyhedra containing both rhombic and triangular faces which are face transitive within the two subsets of faces.
Molybi-pyramids
A 'molybi-pyramid' can be formed by taking a polygon, surrounding it by triangles and then inserting rhombi between the triangles such that the open vertices of the rhombi coincide. The term is my own construction as derives from the Greek word for pencil 'molybi', after the similarity between a hexagonal molybi-pyramid and the point of a lead pencil (see above). An alternate method of construction would be to take a semicupola or sesquicupola, augment the base face with a pyramid, and take the convex hull.
Molybi-pyramids can be formed with a polygonal base {n/d} in the range 2.4 < n/d < 12, with the limiting cases being planar ({12/5}, {12/5}-highlight and {12}).
The acute angles of the rhombi are interesting. For the triangular molybi-pyramid, the rhombi have an acute angle of 60° - and can be thought of as two coplanar triangles. For the pentagonal molybi-pyramid, the rhombi have an acute angle of 36°. There is also a pentagrammic molybi-pyramid where the rhombi have an acute angle of 72°. These, along with the limiting cases, appear to be the only rational values of n/d which produce rational rhombi angles. Two other cases are easy to derive explicitly, the square molybi-pyramid has rhombi with an acute angle of 41.4096° [ 2.tan-1(1/sqrt(7)) ] , and the hexagonal molybi-pyramid has rhombi with an acute angle of 33.5573° [ 2.tan-1(1/sqrt(11)) ].
The Platonic or Kepler-Poinsot polyhedra can be augmented or excavated with molybi-pyramids to form a class of polyhedra which are face transitive within the two subsets of faces. A number of the results however are degenerate.
Molybi augmented Platonic polyhedra
 |
 |
| Molybi augmented tetrahedron: VRML OFF | Molybi excavated tetrahedron: VRML OFF |
 |
Degenerate |
| Molybi augmented octahedron: VRML OFF | Molybi excavated octahedron: |
 |
 |
| Molybi augmented icosahedron: VRML OFF | Molybi excavated icosahedron: VRML OFF |
 |
 |
| Molybi augmented cube: VRML OFF | Molybi excavated cube *: VRML OFF |
 |
Degenerate |
| Molybi augmented dodecahedron: VRML OFF | Molybi excavated dodecahedron: |
* Note: The molybi excavated cube may appear degenerate but the apparently square faces are made up of four coplanar triangles.
Molybi augmented Kepler-Poinsot polyhedra
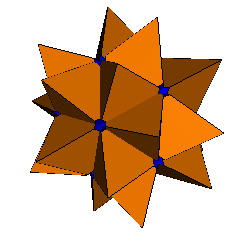 |
 |
| Molybi augmented great icosahedron: VRML OFF | Molybi excavated great icosahedron: VRML OFF |
 |
 |
| Molybi augmented great dodecahedron: VRML OFF | Molybi excavated great dodecahedron: VRML OFF |
 |
 |
| Molybi augmented small stellated dodecahedron *: VRML OFF | Molybi excavated small stellated dodecahedron: VRML OFF |
 |
Degenerate |
| Molybi augmented great stellated dodecahedron: VRML OFF | Molybi augmented great stellated dodecahedron |
* Note: The molybi augmented small stellated dodecahedron may appear degenerate but the apparently pentagonal faces are made up of five coplanar rhombi.
Credits
The molybi-pyramids produced using HEDRON. Augmentation was performed in Great Stella and switch VRMLs produced using Hedron Tools and HEDRON.
Pictures of the {12} and {12-5} molybi-pyramids were produced using Tyler (with some post-processing).