A number of uniform polyhedra can be thought of as being constructed from overlapping cupolas. Obvious cases are the Rhombicuboctahedron being generated from six square cupolas. Rotating a single cupola results in Miller's solid: otherwise known as the elongated square gyrobicupola.

Turning to the 4/3 cupola, it is fascinating to see this as a fragment of uniform polyhedra. For example, the Great Cubicuboctahedron is the union of six 4/3-cupolas with their triangular faces co-incident. Click the image above for a model with one cupola highlighted.

Click here for further discussion on the relationship between the small and great rhombicuboctahedron.

The 5/3 cupola also appears in a number of uniform polyhedra. There are parallels between the appearances of both the ⁴/₃ cupola and the ⁵/₃ cupola. If B1 is used to denote the small cupola base (⁴/₃ and ⁵/₃ respectively) and B2 used to denote the larger cupola base (⁸/₃ and ¹⁰/₃ respectively) then uniform polyhedra exist for both cupolas with (crossed) vertices of the form B1,4,3,4   B2,B1,B2,3   B2,4,B2,4. For the first of these, (with the B1,4,3,4 vertex,) gyrated and diminished forms also exist (see below).

For the specific case of the 5/2 semicupola and the 5/4 semicupola a relationship exists with the ditrigonal polyhedra.  More on that relationship can be found here.

The following table gives all polyhedra fitting the above categories. In all cases below, if the "Hi" following the polyhedron name is clicked then a model is shown in which a single cupola has been highlighted (as in the above image)
 
 

Vertex	4/3 Cupola	5/3 Cupola
B1,4,3,4	Great Rhombicuboctahedron  Hi	Great Rhombicosidodecahedron Hi
B2,B1,B2,3	Great Cubicuboctahedron  Hi	Great Dodecicosidodecahedron  Hi
B2,4,B2,4	Great  Rhombihexahedron  Hi	Great Rhombidodecahedron  Hi

In the case of the B1,4,3,4 polyhedra, as mentioned above, gyrate and diminished forms exist. For the Great Rhombicuboctahedron there is one gyrated form, the Gyrate Great Rhombicuboctahedron  (Hi) (interestingly this polyhedron has all its vertices of the form 4,4,3,4 although it is not uniform). There is also one diminished form, the Diminished Great Rhombicuboctahedron  (Hi)

For the Great Rhombicosidodecahedron ("QRID" from its original name of quasirhombicosidodecahedron) a total of twelve gyrate and diminished forms exist. These are tabulated below in the same sequence as the image. Click on the image or the table to load the VRML files.
 
 
 
 
 

Gyrate (Hi)		Metabigyrate (Hi)		Parabigyrate (Hi)		Trigyrate (Hi)
Diminished (Hi)		Metabidiminished (Hi)		Parabidiminished (Hi)		Tridiminished (Hi)
Metagyrate Diminished (Hi)		Paragyrate Diminished (Hi)		Bigyrate Diminished (Hi)		Gyrated Bidiminished (Hi)

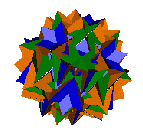Note though that the gyrate forms do not have similar vertices as they contain a mixture of 5/2,4,3,4 and 5/2,4,4,3 vertices.

Another way of seeing the component cupolas in the QRID is to 'evert' one or more of the cupolas by reflecting it in the plane of its base ¹⁰/₃-gon.  A number of models can then be generated.  Those displaying evertion only are these models of the Everted QRID,  Metabi-everted QRID,  Parabi-everted QRID and Tri-everted QRID.  These are all isomorphs of the basic QRID.

As well as evertion, it is also possible to Gyro-evert a cupola.  The cupola is everted as above and then gyrated.  As an example see this Gyroeverted QRID.  Each of these variations is an isomorph to one of the variations in the gyrated/diminished table above.  In total this seems to permit a total of 44 variations to the basic QRID.  Using shorthand notation of G for gyrated, D for diminished, E for everted and GE for gyroeverted, with qualifiers m (meta) and p (para) then the possibilities are tabulated by isomer as follows:
 
 

Base:  QRID Base   E E.Em E.Ep E.E.E
Base:  Gyrate G E.Gm E.Gp E.E.G GE E.GEm E.GEp E.E.GE	Base: Metabigyrate G.Gm E.G.G G.GEm GE.GEm E.GE.GE	Base: Parabigyrate G.Gp G.GEp GE.GEp	Base: Trigyrate G.G.G G.G.GE G.GE.GE GE.GE.GE
Base: Diminished D D.Em D.Ep D.E.E	Base: Metabidiminished D.Dm D.D.E	Base: Parabidiminished D.Dp	Base: Tridiminished D.D.D
Base: Metagyrate-diminished D.Gm D.E.G   D.GEm D.E.GE	Base: Paragyrate-diminished D.Gp D.GEp	Base: Bigyrate-diminished D.G.G D.G.GE D.GE.GE	Base: Gyrate-bidiminished D.D.G D.D.GE

Back: To Cupolas
Back: To Index