
5/4 semicupola and 5/2 semicupola (image courtesy of Christine Tuveson - reproduced with permission)
The 5/2 semicupola and 5/4 semicupola

5/4 semicupola and 5/2 semicupola
(image courtesy of Christine Tuveson - reproduced with permission)
Both the 5/2 semicupola and the 5/4 semicupola can be formed by the judicious sectioning of certain uniform polyhedra.
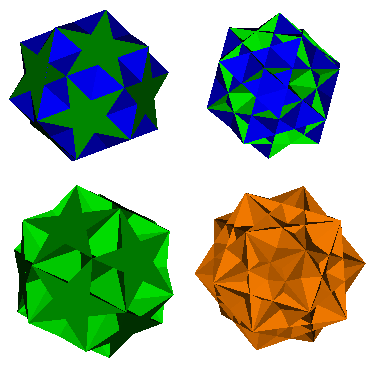
Three uniform polyhedra: the small ditrigonary icosidodecahedron, the great ditrigonary icosidodecahedron and the ditrigonary dodecadodecahedron (shown left to right, top to bottom above) all share the same set of edges, as does the above compound of five cubes (bottom right). The 5/2 semicupola and the 5/4 semicupola can be formed by taking selected faces from these polyhedra.
The small ditrigonary icosidodecahedron consists of pentagrammic and triangular faces. The great ditrigonary icosidodecahedron has the same pentagrammic faces as the small ditrigonary icosidodecahedron but these are now linked with pentagons, the ditrigonary dodecadodecahedron has the triangular faces of the small ditrigonary icosidodecahedron and the pentagonal faces of the great ditrigonary icosidodecahedron. Examination of the small ditrigonary icosidodecahedron also reveals the prospect of square faces. These prove to be the faces of the compound of five cubes (multi-coloured). It is interesting to view this compound within the framework of the small ditrigonary icosidodecahedron (multi-coloured) (image above).
The 5/2 semicupola can be taken as one pentagram (from the above uniform polyhedra) edge connected to five squares (from the compound of five cubes) which are in turn edge connected to five triangles (from the above polyhedra). Models are presented of a 5/2 semicupola within the framework of the small ditrigonary icosidodecahedron (above left) and a 5/2 semicupola within the framework of the compound of five cubes (above right).


The 5/4 semicupola
can similarly be viewed as one pentagon (from the above
uniform polyhedra) edge connected to five squares (from the compound of
five cubes) which are in turn edge connected to five triangles (from the
above polyhedra). Models are presented of a 5/4 semicupola
within the framework of the small ditrigonary icosidodecahedron
(above left) and a 5/4 semicupola within the framework
of the compound of five cubes (above right).


Examination of these models
shows that both semicupolas could be fitted within a single encasing polyhedron.
It is stressed though that the 'compound of a 5/2 semicupola and a 5/4 semicupola'
is not a polyhedron as it has four faces meeting at each edge of the pentagonal
face where the two semicupolas coincide. However, models are presented
of a 5/2 semicupola and a 5/4 semicupola within the
framework of the small ditrigonary icosidodecahedron (above left) and
a 5/2 semicupola and a 5/4 semicupola within the framework
of the compound of five cubes (above right).
The models on this page were inspired by models produced by Ulrich Mikloweit (polyart@citylink.de) on his page at http://www.polyedergarten.de/e_Klintro.htm where he is hosting Doctor Robert Klitzing's catalogue of all the facets of the above polyhedra.
Next: Tables
of Cupolas and Semicupolas
Back: To Semicupolas
Back: To Index