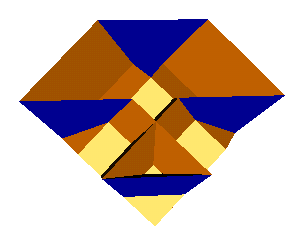
Isomorphs to the Rhombicuboctahedron
This 'space invader' is actually an isomorph of a uniform polyhedron, it shares the same net as the rhombicuboctahedron. It's derivation is described below.

As previously mentioned
in my cupola pages, the small
rhombicuboctahedron above can
be thought of as six overlapping square cupolae.

Were one of these cupolae
to be pushed inwards (or 'inverted') an isomorph to the rhombicuboctahedron
is formed which I name an inverted rhombicuboctahedron
above. Normally when such
an operation is carried out on one face of such a polyhedron, a similar
operation cannot be carried out on any neighbouring faces. The rhombicuboctahedron
however is an exception. The relevant edges of the inverted cupola
remain coplanar with the (now distorted) octagonal face of the neighbouring
cupolae allowing these also to be inverted.
 |
 |
Two variants of the bi-inverted
rhombicuboctahedron exist. A meta-bi-inverted
rhombicuboctahedron above left
where two neighbouring cupolae are inverted, and a para-bi-inverted
rhombicuboctahedron above
right where two opposing cupolae are inverted.
 |
 |
Similarly two tri-inverted
rhombicuboctahedra exist. I term these a meta-tri-inverted
rhombicuboctahedron above left
where three neighbouring cupolae are inverted, and a para-tri-inverted
rhombicuboctahedron above
right where two of the three inverted cupolae are opposed.
 |
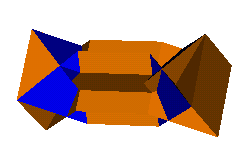 |
For the tetra-inverted rhombicuboctahedron
we one more have two variants. Again the terminology is similar, in this
case the meta-tetra-inverted rhombicuboctahedron
above left has two neighbouring
cupolae left convex (or 'everted') and the para-tetra-inverted
rhombicuboctahedron above right
has two opposing cupolae left everted, these are now {4/3}
cupolae due to the invertion of all the neighbouring cupolae.
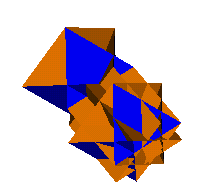
Only one penta-inverted
rhombicuboctahedron above exists
with its one everted 4/3} cupola.

When we come to the hexa-inverted
rhombicuboctahedron above we
arrive at a familiar figure. We have now generated a great
rhombicuboctahedron. This allows us to rename the penta-inverted
rhombicuboctahedron as an everted great rhombicuboctahedron and the tetra-inverted
rhombicuboctahedra as bi-everted great rhombicuboctahedra, this clarifies
the use of the meta and para prefixes for these polyhedra.
Animations
The generation of the great rhombicuboctahedron from the small rhombicuboctahedron by invertion of its cupolae is the subject of the following animated VRML files.
1. All cupolae are inverted together.
2. The cupolae are inverted serially (meta route).
3. The cupolae are inverted serially (para route).
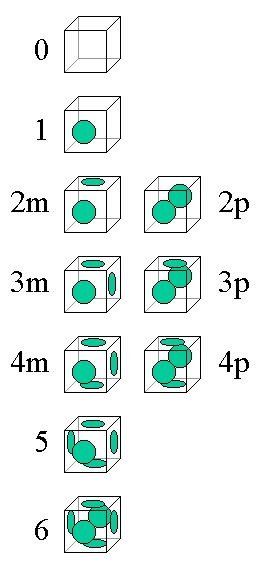
Equivalence to cube colourings
A feature of the above isomorphs to the rhombicuboctahedron is that they illustrate the ten distinct ways in which a cube can be coloured using two colours for the faces, as shown in the diagram below. The plain faces relate to everted cupolae and the faces with green blobs to inverted cupolae.
ps. the 'space invader' could be either the meta-tri-inverted rhombicuboctahedron (if you want a back to his head) or a meta-tetra-inverted rhombicuboctahedron (if you prefer a two-faced version).