

Honeycombs derived from the octahedral/tetrahedral honeycomb, Page 1
10Y4-8T-n
 |
 |
 |
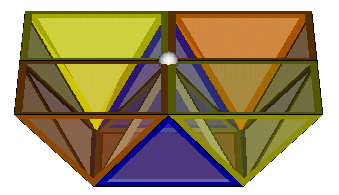
The simplest elementary honeycomb is formed by taking the regular honeycomb (6S3-8T) and bisecting all of the octahedra into two square prisms with parallel planes. As the bisection of the octahedra affects four octahedra at each honeycomb vertex, the honeycomb formed is denoted (10Y4-8T-n). (The 'n' is required as other honeycombs with similar vertices will be met later on). The top left hand image above shows one half-vertex of this honeycomb, note how four base vertices from the square pyramids are adjacent to the marked honeycomb vertex along with one apex vertex from the square pyramid which has it's square face at the base of the image. The top right hand image shows half-vertices on two adjacent planes. Note how the four square pyramids contributing base vertices from the first image each contribute an apex vertex to a different honeycomb vertex on the second plane. Finally, in the bottom image two half-vertices joined together complete the structure around the vertex. Note: all of the VRML files linked from images on this page are HEDRON 'switch' files. Click on the 'trans' button at the base of the screen to see the internal structure of the vertices.
 |
 |
The above honeycomb (10Y4-8T-n) can be 'elongated' by the addition of a layer of cubic cells between each layer of pyramids and tetrahedra. This is easiest to see by taking the top left image of a half vertex from the 10Y4-8T-n and superposing the layer of cubes to give the top right image. The overall vertex formation now becomes 5Y4-4T-4P4.
5Y4-4T-6P3-sq-gyro and 5Y4-4T-6P3-sq-ortho
An alternative to the above elongation
is to
insert a later of triangular prisms.
Six
prisms are required at each vertex. These layers can be
included in
one of two ways, either the layers can be placed such that the prisms
are
parallel 5Y4-4T-6P3-sq-gyro
- above left,
or such that the prisms are perpendicular 5Y4-4T-6P3-sq-ortho
- above right. The insertion of the text 'sq' is in order to
distinguish
these modes, formed from layers with exposed square faces, from further
modes (see
here) formed from layers with exposed triangular faces. In
order to see the difference between the two, it is
necessary to complete two vertices of the honeycomb.
Incidence matrices for all the above
honeycombs are given by Richard Klitzing here.
Next: Honeycombs derived from the octahedral/tetrahedral honeycomb, Page 2
Back: To honeycombs index
Return: To main index
[1] George Olshevsky
[2] Banko Gr�nbaum in "Uniform tilings of 3-space," Geombinatorics 4, 49-56 (1994)
[3] Alex Doskey
[4] Peter Cromwell, "Polyhedra"
[5] Johnson Solids