
5Y4-4T-6P3-tri-n
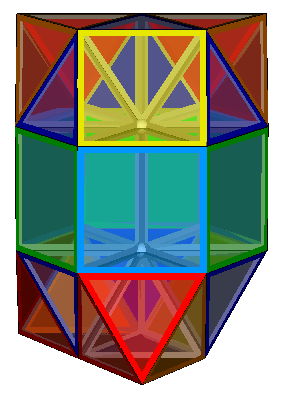
5Y4-4T-6P3-tri-ortho
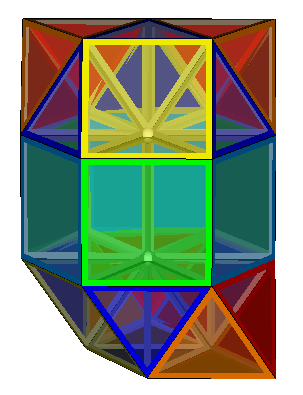
5Y4-4T-6P3-tri-meta
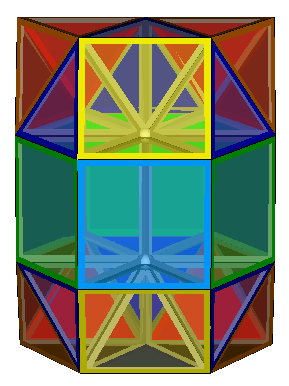
5Y4-4T-6P3-tri-para
Honeycombs derived from the octahedral/tetrahedral honeycomb, Page 3
The four honeycombs described on the previous page, 10Y4-8T-n, 10Y4-8T-ortho, 10Y4-8T-meta and 10Y4-8T-para can also be elongated by the insertion of layers of triangular prisms between each layer of pyramids and tetrahedra. The four equivalent honeycombs then become 5Y4-4T-6P3-tri-n, 5Y4-4T-6P3-tri-ortho, 5Y4-4T-6P3-tri-meta and 5Y4-4T-6P3-tri-para. The insertion of the 'tri' in the name is to distinguish these from the previously discussed 5Y4-4T-6P3-sq-ortho and 5Y4-4T-6P3-sq-gyro formed from layers with square faces exposed.
The table below shows all four modes with the same colour coding as previously.

5Y4-4T-6P3-tri-n |

5Y4-4T-6P3-tri-ortho |

5Y4-4T-6P3-tri-meta |

5Y4-4T-6P3-tri-para |
As on the
previous page, the ortho and meta modes each have two forms, an
alternating form where the gyrations of pi/3 or 2pi/3 respectively
alternate back and forth, and a helical form where the gyrations
continue in the same direction. (Discovered by Richard Klitzing, 2013).
Incidence matrices for all the above honeycombs are given by Richard Klitzing here.
Next: Honeycombs derived from the runcinated alternated cubic honeycomb
Back: To honeycombs index
Return: To main index