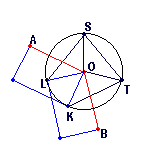
Fig 1 (k,w) = (3,0)
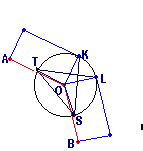
Fig 2 (k,w)=(3,1)

The edge expanded bi-prisms ("EEB's") are a set of families of prismatic polyhedra. They are formed by the insertion of triangular faces between the square (prismatic) faces of a prism of height 2. The general EEB and the calculation of its height was first described by Dr Richard Klitzing on 1 June 1999 in the correspondence linked here.
Take a standard prism. Insert one triangle between each of the square faces. The result (for a prism of {n/d} < 6) is a cupola. Take two such cupolas and join them by their large bases (edge of square face to edge of square face) to form an ortho-bi-cupola. This is an EEB of order 1 or an edge (mono-)expanded bi-prism.
Repeating the exercise of inserting triangles gives the possibility of two polyhedra. The triangular faces may either extend outwards from the base polygon - in which case the square faces tend to face inwards (an 'exo' edge bi-expanded bi-prism) or the triangular faces can face inwards - in which case the square faces tend to face outwards (an 'endo' edge bi-expanded bi-prism). The equatorial polygons are now no longer regular; this is the reason why two prisms are used rather than one. Reflecting the prism through the equatorial plane allow for closure of these non-regular polygons.
The exercise of inserting
triangles can be repeated again. For the edge tri-expanded bi-prisms
another possibility occurs. For each of the endo and exo modes, the
triangular faces can be inserted in one of two ways, either crossed or
uncrossed. However, with higher order EEB's, I find it easier to
define a 'winding number' (w). For a non-wound EEB the triangular
faces fill the angle between two square faces (fig 1), a 'wound'
EEB has the triangular faces filling the angle between the square faces
plus an angle of 2.pi times w (fig 2). In traversing the triangles,
count counter clockwise from K through S then T to L.

Fig 1 (k,w) = (3,0) |

Fig 2 (k,w)=(3,1) |
In general, it appears that an edge k-extended bi-prism can have 0 <= w <= (k-1). See below for more details of limitations.
In full then, each individual polyhedron can be named an {n/d} [endo / exo] edge k-expanded w-wound bi-prism where {n/d} identifies the base polygon. In short, I refer to this as an {n/d} [endo/exo] (k,w) EEB. The exo (2,1) EEB is a special case in that it is locally convex for 2 < {n/d} < 3. I previously termed these solids 'spheno-prisms'. For further discussion of these particular solids and their local convexity, click here.
The height (h) of an {n/d} [endo/exo] (k,w) EEB is given by
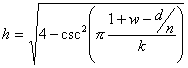
Click here for proof. Note that the height is the same for both the endo and exo modes.
A graph plotting the heights of various EEB's against n/d is informative as it shows EEB's of differing (k,w) sharing a height at rational values of n/d. For example (k,w) of (1,0) (2,0) (4,2) and (5,1) all have the same height at n/d = 3 implying a number of toroidal possibilities. It is fascinating to see heights of (3,0) and (4,2) coincide at n/d = 7. Click HERE for the graph and further discussion of this possibility.
Summarising the graph to show the range of n/d > 1 for which EEB's of varying (k,w) exist gives the following list:
(k,w)
(1,0)
6/5 < n/d < 6 (i.e. cupolas)
(2,0)
n/d> 3/2
(2,1)
n/d < 3
(3,0)
n/d > 2
(3,1)
all n/d
(3,2)
n/d < 2
(4,0)
n/d > 3
(4,1)
all n/d
(4,2)
all n/d
(4,3)
n/d < 3/2
(5,0)
n/d > 6
(5,1)
all n/d
(5,2)
all n/d
(5,3)
all n/d
(5,4)
n/d < 6/5
Models have been generated where the EEB exists for n/d=7 and k<=5. Three alternatives are presented for each mode. A 'solid' model (which tends to be dominated by the square faces in endo mode and by the triangular faces in exo mode), a 'frame' model where the base heptagons have been replaced by heptagonal frames to show the internal structure, and a 'hemi' model showing just half of the polyhedron with equatorial edges highlighted. These are probably the best option for understanding the internal structure of the polyhedron.
The diagrams shown below are of the equatorial edges with square edges in light blue and triangular edges in dark blue. The projection of the base vertices onto the equatorial plane are shown in red. Clicking on the diagrams leads to the 'hemi' models. The 'toroid' links lead to the toroids formed by superposing an endo and an exo model and removing the heptagonal bases.
{7} (k/w) EEBs
{7} endo (2,0) EEB
solid, frame |
{7} exo (2,0) EEB
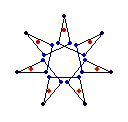
solid, frame, toroid |
{7} endo (3,0) EEB
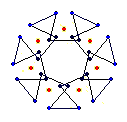
solid, frame |
{7} exo (3,0) EEB
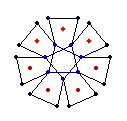
solid, frame, toroid |
{7} endo (3,1) EEB
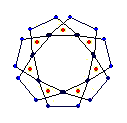
solid, frame |
{7} exo (3,1) EEB
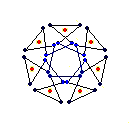
solid, frame, toroid |
{7} endo (4,0) EEB
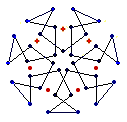
solid, frame |
{7} exo (4,0) EEB
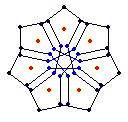
solid, frame, toroid |
{7} endo (4,1) EEB
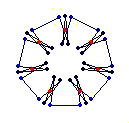
solid, frame |
{7} exo (4,1) EEB
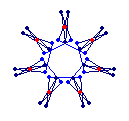
solid, frame, toroid |
{7} endo (4,2) EEB
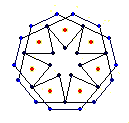
solid, frame |
{7} exo (4,2) EEB
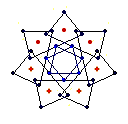
solid, frame, toroid |
{7} endo (5,0) EEB
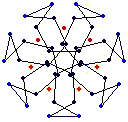
solid, frame |
{7} exo (5,0) EEB
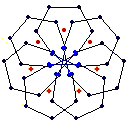
solid, frame, toroid |
{7} endo (5,1) EEB
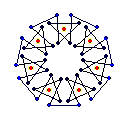
solid, frame |
{7} exov (5,1) EEB
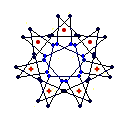
solid, frame, toroid |
{7} endo (5,2) EEB
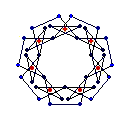
solid, frame |
{7} exo (5,2) EEB
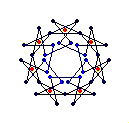
solid, frame, toroid |
{7} endo (5,3) EEB
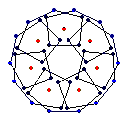
solid, frame |
{7} exo (5,3) EEB
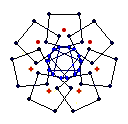
solid, frame, toroid |
It would appear from the above that the (k,w) = (4,2) and (5,2) cases contain superposed vertices. Closer analysis shows that these vertices are within 1x10E-15 of each other, but I have not proved they are superposed. Strangely this only appears to be the case for n/d=7, setting n/d to 6 or 8 shows the vertices as clearly distinct.
This can be seen from the linked Excel 97 Spreadsheet (here). This spreadsheet was used (rather than my usual "hedron" program) to generate the above diagrams and the co-ordinates for the linked models. Whilst not totally flexible, it does allow for some variation in n/d and for values of k up to 12. For an example of its output see then diagram of the (12,5) case below:
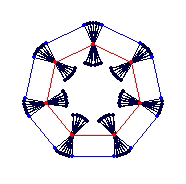
I have used the spreadsheet to generate diagrams for n/d = 7/6. In these cases, the w=0 models do not exist, rather than the w=k-1 models for the n/d=7 case. There also appears to be a relationship that the {7} exo/endo (k,w) EEB is equivalent to the {7/6} endo/exo (k,(k-1)-w)) EEB, (e.g. the {7} endo (4,1) EEB is equivalent to the {7} exo (4,2) EEB ) so diagrams of all the {7/6} EEBs are contained in the table above.
Next: Heterogenous
EEB Toroids
Back: Main