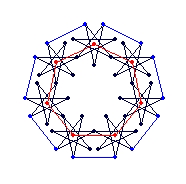
One hemisphere of a {7} endo (5,2) / exo (2,0) EEB with equatorial edges highlighted

A graph plotting the half-heghts against n/d for varoius EEB's for k <= 5 is as follows

Clicking on the graph will display a magnified version.

As well as displaying the limits of the various values of (k,w), the graph shows that at certain values of n/d, the neights of two different (k,w) can co-incide.
An obvious example being the crossing of (k,w) = (1,0) and (4,0) at n/d = 5.

The lines can cross in one of two ways, either case (i) both lines can be increasing / decreasing, or case (ii) lines can be moving in different directions.

From the height of the EEB:

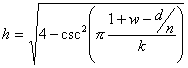
If the height is shown as

In case (i), simply set

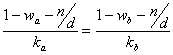
to obtain the value of {n/d} at which the height of EEBs (k_a,w_a) and (k_b,w_b) coincide at:

In case (ii), use the relationship

to obtain

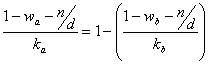
rearrange to obtain the value of n/d at which the height of EEBs (k_a,w_a) and (k_b,w_b) coincide at:

In both cases n/d will be rational.

This value can be tabulated for various(k,w), although care must be taken that the resulting value is within the range of the EEB in question.  The table below shows those values of n/d>1  Values in red (italics) are obtained from case (i), those in black are obtained from case (ii):
 

	(1,0)	(2,0)	(2,1)	(3,0)	(3,1)	(3,2)	(4,0)	(4,1)	(4,2)	(4,3)	(5,0)	(5,1)	(5,2)	(5,3)	(5,4)
(5,4)
(5,3)	3/2, 4	7/3	3/2	4	8/7		9	3/2			Infinity	2
(5,2)	2, 2	7	7/6		2, 2			9/2	9/7			Infinity
(5,1)	4/3, 3	3	7/4		8	4/3			3	9/8
(5,0)
(4,3)	5/4
(4,2)	5/3, 3	3		7	7/5		Infinity	2
(4,1)	3/2, 5/2	Infinity	3/2		7/2	7/6
(4,0)	5
(3,2)	4/3
(3,1)	2, 2		5/4	Infinity
(3,0)	4		5/2
(2,1)	3/2
(2,0)	3
(1,0)

At the specified n/d, both EEB's have equal heights.  This implies that a 'heterogenous EEB toroid' can be formed by combining one copy of each (k,w) and removing the superposed base faces.  At first glance, four models are possible for each toroid, an exo/exo model, an exo/endo model, an endo/exo model and an endo/endo model.  However as the heights are the same then the square faces of the endo/endo model are superposed (likewise the exo/exo model) leaving only the endo/exo and the exo/endo models.

Case (i) toroids prove to be the less interesting of the two, the (k_b - k_a) numerator means higher orders of k need to be used to obtain a specific n/d.  In the case of n/d = 7 the lowest values appear to be (9,3) and (2,0).  However, when (9,3) is examined the triangular faces form a {7,3} bi-pyramid with certain faces traversed twice, these faces are precisely those of the (2,0).   Vertex diagrams of both polyhedra are shown below.
 

{7} endo (9,3) EEB

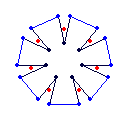
{7} endo (2,0) EEB

the triangular faces of the (2,0) are then superposed 3 times in the resulting toroid.

For case (ii), interesting toroids can be generated at lower values of k avoiding the superposed faces of the case (i) examples.  Toroids examples are given for the two sets of toroids for which n/d = 7.  For nomenclature, I utilise a form of Stewart Toroid nomenclature and refer to each toroid as an {n/d} [endo/exo] (k_a,w_a) / [endo/exo] (k_b,w_b) EEB.  As previously, 'solid' models tend to be dominated by the square faces so 'hemi' models showing half of the polyhedron (and the internal construction) are given.  Whilst the endo/endo and exo/exo models have superposed faces, they are included below as they show the complimentary nature of (k_a,w_a) and (k_b,w_b) as the union of the triangular faces forms in the first case {7/2} bi-pyramids and in the second case {7/3} bi-pyramids.

The EEB's used in the constructions are these:

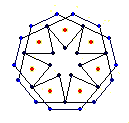
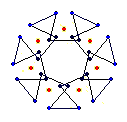
{7} endo (4,2) EEB	{7} endo (3,0) EEB
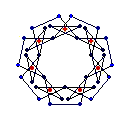
{7} endo (5,2) EEB	{7} endo (2,0) EEB

Giving rise to toroids:

{7} endo (4,2) / exo (3,0) EEB solid, hemi	{7} exo (4,2) / endo (3,0) EEB solid, hemi	{7} endo (4,2) / endo (3,0) EEB solid, hemi	{7} exo (4,2) / exo (3,0) EEB solid, hemi
{7} endo (5,2) / exo (2,0) EEB solid, hemi	{7} exo (5,2) / endo (2,0) EEB solid, hemi	{7} endo (5,2) / endo (2,0) EEB solid, hemi	{7} exo (5,2) / exo (2,0) EEB solid, hemi

All of the heterogenous EEB toroid forms explored to date involve superposed vertices, and likewise all EEB's containing superposed vertices appear to be a participant in a heterogenous EEB toroid.  I have not determined whether the occurance of one necessarily implies the other.

Back: to EEBs