Well [...] back to cupolae.

If one reflects those at their basis one would get bicupolae.
In the same sense I would call biprisms such which would be got if one
joins two at their base, i.e. put them ontop of another (just to have a name).

The connex between those two bi's is clear: both consist of identical top
and base faces; both join the polar circle (meaning the edge circuit of the
former faces) by means of squares to the equator. Just inbetween these
lateral edges is a little difference: in case of biprisms is nothing
inbetween, in case of bicupolae is (a reflected pair of) one triangle
inbetween.

Jim McNeill recently pointed out to me in a private mail, that he has found
a thing, which could be implemented into the above setup by fitting (a
reflected pair of) _two_ triangles inbetween. (He called these solids
spheno prisms, as the parts inbetween the polar faces reminds him to the
spheno-... called Johnson polyhedra).

Here it becomes clear why I've doubled things by reflection, as the
equatorial intersection of these "edge-expanded biprisms of degree 2" are
no longer regular polygons, like the cases of degree 1 (being bicupolae) or
0 (being biprisms).

But of course, we don't have to stop at degree 2.
The only conditions to the lateral triangles are the sequential connection,
and that the opposite edges of them with respect to the polar vertex have
to lie all within a single plane (the equatorial one).

In order to reduce too much freedom, one should additionally restrict
oneself to the cases which have still the full symmetry of the original
biprism. (No chiral stuff.)

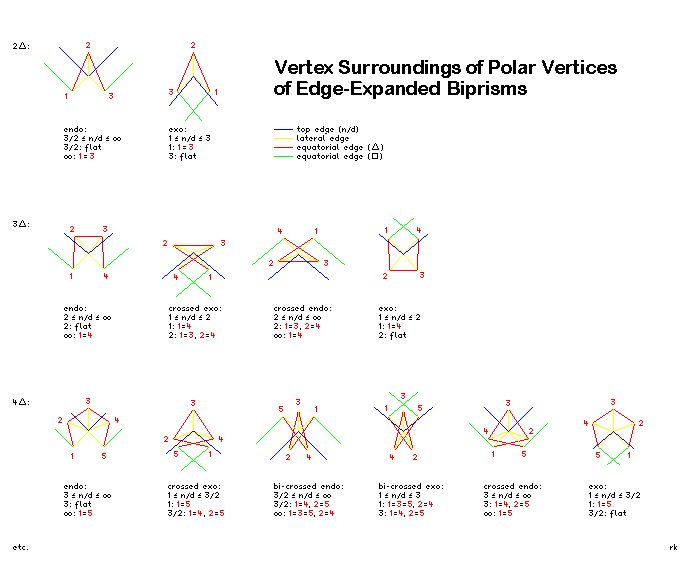
I append a handdrawn bitmap (about 400k) of the different kinds of polar
vertex configurations for edge-expanded biprisms (EEBs) of degree 2, 3, and
4. I think that these first steps of induction make things quite clear.

Dr Richard Klitzing   02/06/1999    appended here with permission

Yesterday I've posted some notes on EEBs (edge-extended biprisms). Now I've
calculated their heights as well.

Squared height of endo EEB of order k is
4 - csc^2 (180*(1 - d/n)/k)
...
Squared height of exo EEB of order k is
4 - csc^2 (180*(k - d/n)/k)

Inbetween: for each crossing of the lateral edges of the original biprism
(ment as sequance of pictures within each line marked "1" and "k+1" in my
yesterday bitmap) one has to add 1 in the inner paranthesis.

Therefore e.g.:
squared height of crossed exo EEB(3) = squared height of crossed endo
EEB(3) =
4 - csc^2 (180*(2 - d/n)/3),
squared height of crossed exo EEB(4) = squared height of bi-crossed endo
EEB(4) =
4 - csc^2 (180*(2 - d/n)/4),
squared height of bi-crossed exo EEB(4) = squared height of crossed endo
EEB(4) =
4 - csc^2 (180*(3 - d/n)/4),
etc., and of course
squared height of EEB(1) = squared height of bi-cupola =
4 - csc^2 (180*(1 - d/n)/1) = 4 - csc^2 (180*d/n)

(Hence, as an easy necessary condition of existance one should calculate
the squared height and check wether it isn't negative.)

--- rk
 
 

  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

  Dr. Richard Klitzing  :klitzing@swh600.langen.bull.de

  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~