
Toroids involving Edge Expanded Bi-anti-prisms (EEAs) can be grouped into three categories. The first is a set of EEA / EEA toroids equivalent to the EEB / EEB toroids discussed previously (see here). The others are two categories of EEA / EEB toroids. The first of these, I term 'specific' EEA / EEB toroids, these are again equivalent to the EEB / EEB toroids with one EEB replaced by an EEA of the same height. The second set is termed (by me) 'generic' EEA / EEB toroids, unlike the other sets they do not just occur at specific values of n/d but occur over a range of n/d. These three sets are discussed below:
EEA / EEA Toroids.
The height of an EEA is given by
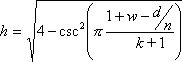
The above formula is very similar to that describing the height of an EEB. In similar fashion to the EEB logic (here), it can be shown that EEAs of differing values of (w,k) are of equal height at specific values of n/d. However as there is only one EEA at a specific (w,k) rather than the two EEBs, having equal heights at a particular n/d only gives rise to one toroid rather than the four variations that occur for EEBs.
Searching for toroids at n/d=7 gives two options, a (1/0) / exo (4/1) EEA toroid (not modelled) and an endo (2/0) / exo (3/0) EEA toroid shown above and also linked below. This is the first polyhedron I have come across that exists only with a seven-fold symmetry and is also clear of the superposed vertices and/or faces which plague the EEB / EEB toroids.
Note: as in all the models linked on this sheet, diagrams are shown of the equatorial edges. Clicking on the diagrams leads to 'semi' models showing just one hemisphere. The toroid name underneath each diagram links to a model of the complete toroid. The colour schemes are as follows: triangular faces which are edge connected to the original prismatic base are shown in yellow. Other triangular faces are in blue. For EEB models, square faces are orange.
Generic EEA / EEB Toroids.

These are formed in similar
fashion to the above, except that now instead of two different EEAs, the
height of an EEB and an EEA are equated. Where the heights are equal
then two toroids result, an 'EEA / exo EEB' and an 'EEA / endo EEB'.
The most obvious solution is gained from a simple examination of the heights of the EEAs and EEBs. This shows that the height of an (k,w) EEB is equal to that of a (k+1,w) EEA. As the heights of endo-EEBs and exo-EEBs are equal this gives two toroids for each value of (k,w).
Note that these toroids exist for all values of n/d where the component EEA and EEB exist.
Results at n/d=7 for k=2
to k=4 are shown in the table below. See above for the colour scheme. A
further and unintended further piece of information comes from the triangular
faces, the darker blue faces are at a more acute angle to the cut plane.
Specific EEA / EEB Toroids.

Other specific toroids can be generated by searching for EEA / EEA
solutions other than the generic one given above. This results in toroids
which only exist at a specific value of (n/d). Searching for results
at (n/d) = 7 revealed one specific example, the height of the endo (2/0)
EEA and the (4/2) EEB (both endo- and exo- versions) are equal. The
links below are to the resulting toroids:

endo (2/0) EEA / endo (4/2) EEB |

endo (2/0) EEA / exo (4/2) EEB |
Back: Main