Isohedral Deltahedra

This page contains an exploration of the possibilities for isohedral deltahedra, i.e. polyhedra which are face transitive and consist of equilateral triangular faces.  A total of 34 isohedral deltahedra and one infinite family of deltahedra are presented.  A systematic treatment of isohedral deltahedra can be found in Shephard [1], to which cross references are provided, there are 6 further examples on this page that are not included in Shephard.

Deltahedra from Uniform Polyhedra

Four isohedral deltahedra appear amongst the platonic and Kepler-Poinsot polyhedra

Tetrahedron  Shephard:T2(2)	Octahedron Shephard:O7
Icosahedron Shephard:I11(1)	Great Icosahedron Shephard:I10(1)

Deltahedra From Johnson Solids

Two further isohedral deltahedra appear amongst the Johnson Solids:

Triangular Bipyramid Shephard:D3(1)

Pentagonal Bipyramid Shephard:D5(1)

Extending these figures to consider re-entant polyhedra, the family of {n/d}-bipyramids consists of isohedral deltahedra within the range 2 < n/d < 6.  As  examples, see this {7/2}-bipyramid and {7/3}-bipyramid.  In Shephard's notation, these are case 1, Dn(d)

Deltahedra from Augmented Uniform Polyhedra

Each of the platonic and Kepler-Poinsot polyhedra can potentially be augmented or excavated with pyramids.   A number of the figures are degenerate.  Overall 15 isohedral deltahedra are formed.

Tetrahedron	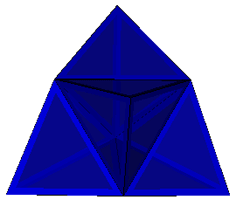Augmented  Triakis Tetrahedron Shephard:T2(1)	degenerate see Tetrahedron
Octahedron Triakis Octahedra	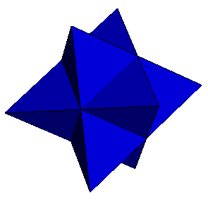Augmented Stellar Octangula Shephard: O6(1)	Excavated Shephard: O6(2)
Cube Tetrakis Hexahedra	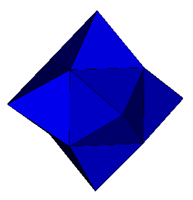Augmented Shephard: T1(1) & O5(1)	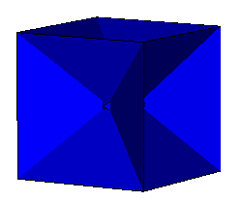Excavated Shephard: T1(2) & O5(2)
Icosahedron Triakis Icosahedra	Augmented Shephard: I6(1)	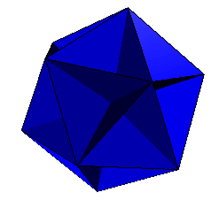Excavated Shephard: I6(2)
Dodecahedron Pentakis Dodecahedra	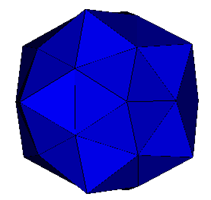Augmented Shephard: I9(1)	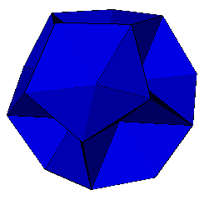Excavated Shephard: I9(2)
Great Icosahedron Triakis Great Icosahedra	Augmented Shephard: I7(2)	Excavated Shephard: I7(1)
Great Dodecahedron	degenerate see Icosahedron	Excavated Pentakis Great Dodecahedron Shephard: I11(2)
Small Stellated Dodecahedron	Augmented Triakis Small Stellated Dodecahedron Shephard: I10(2)	degenerate see Great Icosahedron
Great Stellated Dodecahedron Pentakis Great Stellated Dodecahedra	Augmented ** Shephard: I8(1)	Excavated   Shephard: I8(2)

** The deltahedron derived from augmenting the great stellated dodecahedron superficially resembles great icosahedron but each icosahedral face contains three coplanar triangles.

A number of the above deltahedra are also Cundy deltahedra, being concave acoptic (non self-intersecting) deltahedra with two kinds of polyhedron vertices.  These have been enumerated by Roger Kaufman,  who has also investigated their coptic (self-intersecting) variants.  All of the above polyhedra fall into one of these two classes.  The remaining deltahedra listed below all have three types of vertex.

Deltahedra from Deformed Augmented Duals of Tetra-valent Semi-regular Polyhedra - and the Möbius Deltahedra

Apart from the cube, which is discussed above, there are four other rhombic polyhedra which have the property of being edge-transitive.  These are all duals of tetra-valent semi-regular polyhedra.  These can each be augmented or excavated with pyramids to form non-regular deltahedra.  These can all then be deformed such that the faces become equilateral triangles.  Face transitivity is retained in all cases.   The 8 isohedral deltahedra formed in this fashion are listed below, four of which are not included in Shephard.  

Rhombic Dodecahedron	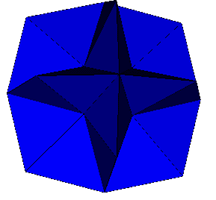Augmented  Octakis Hexahedron Möbius 48A Shephard: O2(2)	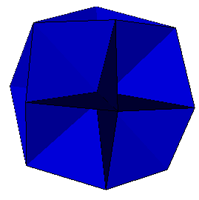Excavated Hexakis Octahedron Möbius 48B Shephard: O2(1)
Rhombic Triacontahedron	Augmented Hexakis Icosahedron Möbius 120A Shephard: I1(2)	Excavated 10-akis Dodecahedron Möbius 120B Shephard: I1(1)
Medial Rhombic Triacontahedron	Augmented   Vert Shephard: not present see [1]	Excavated   Vert Shephard: not present see [2]
Great Rhombic Triacontahedron	Augmented Shephard: not present see [3]	Excavated Shephard: not present see [4]

The text 'Vert' next to the models of the medial rhombic triacontahedron leads to VRML files with the vertices highlighted.  Switching to frame mode and zooming into the centre of the polyhedra shows the configurations of the inner vertices.

There is a set of five isohedral deltahedral figures known as Möbius Deltahedra.  Melinda Green discusses these figures at http://www.superliminal.com/geometry/deltahedra/deltahedra.htm and Roger Kaufman at http://www.interocitors.com/polyhedra/Deltahedra/Mobius/index.html.  Four of these figures can be obtained by augmenting or excavating the rhombic dodecahedron and rhombic triacontahedron as above.  The fifth is a 24 faced figure isomorphous to the augmented cube (image below), it is not derived from any rhombic figure.  The remaining 4 deltahedra are derived from the medial rhombic triacontahedron and great rhombic triacontahedron.

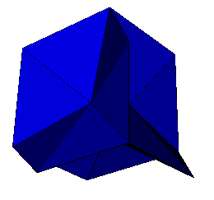
Mobius 24A
Shephard: T1(3)

Deltahedra from Deformed Augmented Duals of Hexa-valent Semi-regular Polyhedra

The semi-regular ditrigonary polyhedra - with vertex figures of (m,n,m,n,m,n) - have duals which consist of hexagonal faces and are also edge transitive.  The above process of augmentation/excavation and deltification can also be applied to these figures.  Some of the resulting figures are degenerate.  The 3 further deltahedra that result are included in the table below.

Uniform Polyhedron
Ditrigonary Dodecadodecahedron (Dual)	Augmented Shephard: I5(1)	Excavated     Vert Shephard: I5(2)
Small Ditrigonary Icosidodecahedron   (Dual)	Degenerate  see Augmented Dodecahedron	Excavated Shephard: I9(3)
Great Ditrigonary Icosidodecahedron (Dual)	Degenerate  see Augmented Great Stellated Dodecahedron	Degenerate  see Excavated Great Stellated Dodecahedron

Deltahedra from Deformed Duals of Trivalent Uniform Polyhedra

A number of the uniform polyhedra are tri-valent, i.e. they have three faces meeting at each vertex.  If the platonic and Kepler-Poinsot polyhedra are excluded (as they are considered above), the remainder have duals with non-regular triangular faces.  These duals can be deformed such that the faces become equilateral triangles.  Face transitivity is retained in all cases.  The 1 new isohedral  deltahedron that results is included in the table below.

No	Vertex	Name ...................................
07	6,6,3	Truncated Tetrahedron	see Augmented Tetrahedron
13	6,6,4	Truncated Octahedron	see Augmented Cube
14	8,8,3	Truncated Cube	see Augmented Octahedron
16	8,6,4	Truncated Cuboctahedron	see Deltified Augmented Rhombic Dodecahedron
21	8/3,6,8	Cubitruncated Cuboctahedron	degenerate see Augmented Octahedron
24	8/3,8/3,3	Stellatruncated Cube	see Excavated Octahedron
25	6,4,8/3	Great Truncated Cuboctahedron	see Deltified Augmented Rhombic Dodecahedron
30	6,6,5	Truncated Icosahedron	see Augmented Dodecahedron
31	10,10,3	Truncated Dodecahedron	see Augmented Icosahedron
33	10,6,4	Truncated Icosidodecahedron	see Deltified Augmented Rhombic Triacontahedron
42	10,10,5/2	Great Truncated Dodecahedron	see Augmented Small Stellated Dodecahedron
50	10,6,10/3	Icositruncated Dodecadodecahedron	see Deltified Excavated Ditrigonary Dodecadodecahedron Dual *
60	6,6,5/2	Great Truncated Icosahedron  (Dual)	see Augmented Great Stellated Dodecahedron
63	10/3,10/3,5	Small Stellatruncated Dodecahedron	see Excavated Great Dodecahedron
64	10,10/3,4	Stellatruncated Dodecadodecahedron	see Deltified Excavated Medial Rhombic Triacontahedron  *
71	3,10/3,10/3	Great Stellatruncated Dodecahedron	see Excavated Great Icosahedron
73	6,10/3,4	Stellatruncated Icosidodecahedron  (Dual)	Deltified Dual Shephard: not present see [5]

Notes:

* The deltahedra derived from excavating the medial rhombic triacontahedron and dual of the ditrigonary dodecadodecahedron duals are similar in appearance.  They are distinct and have different nets.  The distinction is best seen by following the above links to 'Vert', switching to 'frame' view and zooming on the centres of the polyhedra.

Further Examples not in Shephard

The above deltahedron is noted by Shephard as case I7(3).  It was not generated by any of the methods described above.

In February 2008, Adrian Rossiter conducted an exercise using his Antiprism software which effectively performed a systematic repeat of Shephard's calculations . Adrian discovered all of the above figures (including those absent from Shephard) plus one additional figure, which in Shephard fashion he denotes I3(4) (see [6]).  

Examples not included in Shephard

Shephard style notation for these figures:

The Excel spreadsheet linked here contains a full suite of data in the above style for all isohedral deltahedra.

References

[1] Shephard G.C. (1999) Isohedral Deltahedra, Periodica Mathematica Hungarica Vol. 39 (1-3), 83-106

Credits

I am grateful to Professor G.C. Shephard for kindly providing a copy of his paper [1] above, and to Mason Green for inspiring this page by suggesting that the list of isohedral deltahedra, consisting of the top three sections above plus the Möbius Deltahedra, may not be complete.

I am also grateful to Adrian Rossiter and Roger Kaufman for an enlightening exchange of correspondence leading up to and during Adrian's recent exercise (Feb 2008)

A number of the original dual figures were produced using Great Stella and relaxed using HEDRON.

Return: To main index