

In his book "Adventures Among the Toroids" (ISBN 0-686-119 36-3), Professor B.M. Stewart provides a study of "quasi-convex, aplanar, tunnelled, orientable polyhedra having regular faces with disjoint interiors". To classify as a "Stewart Toroid" a polyhedron ("P") must fulfil the following requirements:
(R): Each face of
P must be regular
(A): Faces of P which
share an edge must not be coplanar
(Q): It must be "quasi-convex",
i.e. every edge of the convex closure of P is an edge of P.
(T): P must be tunnelled.
i.e. P contains an excavation which amends the genus of P
The faces of P must also not intersect. So polyhedra containing pentagrams and other star-polygons are excluded.
The notation used in Professor Stewart's
book to describe the toroids is fairly simple. The notation A / B
means the convex closure is polyhedron A and an excavation has been
made to remove polyhedron B. Where the notation reads
A
/ nB(C) then nB means that n excavations have been made
to remove polyhedra B and a central excavation has been made to
remove polyhedron C. The prefix g is used to mean that one
copy of a polyhedron has been gyrated with respect to another. Multi-tiered
toroids have an extended notation of the form A / (B / C), in these
cases polyhedron C has been removed from polyhedron
B, the
resulting toroid B / C is then removed from polyhedron
A.
In effect a C shaped "rod" is inserted into the
B shaped
"hole" in A.
The individual polyhedra utilised below are described using shorthand notation (as used by Stewart) as follows:
B4: cuboctahedron
E4: rhombicuboctahedron
K3: truncated
octahedron
K4: truncated
cuboctahedron
P3: triangular
prism
P4: cube
P6: hexagonal
prism
Q3:
triangular cupola
Q4: square
cupola
Q5: pentagonal
cupola
R5: pentagonal
rotunda
S3: octahedron
S5: pentagonal
anti-prism
T3: truncated
tetrahedron
T4: truncated
cube
J91: bilunabirotunda
Z4: Stewart 'Z4'
For those (simpler) Stewart Toroids that have been modelled, two models are presented:
(i) a 'switchable' model
with all faces following the solid -> translucent -> frame cycle
(ii) a 'combo' model
where the convex closure is as above and the excavation is left solid.
The references to page numbers are to the relevant page in Stewart's book (2nd edition).
To start, two toroids that are NOT Stewart Toroids. They are not quasi-convex and they also break the non-intersecting face rule. They are included here as with just 12 faces, I believe them to be the least faced toroids that can be generated with regular faces. The least faced Stewart Toroid ( Q3P6 / P3Q3 - see third image below) has 21 faces. The first of the 12 faced toroids (left hand image) consists of two hexagonal prisms, one gyrated with regard to the other. Using Stewart notation it is a P6 / gP6. The second (right hand image) (solid, frame) is a faceting of the icosahedron, discovered by Dr Richard Klitzing during a systematic search of such facetings. This second toroid also appears to be the toroid with the least vertices, having just 12. More of Dr Klitzing's images are hosted by Ulrich Mikloweit here
Turning now to Stewart Toroids, amongst the simpler ones are:

Q3P6 / P3Q3 (page
24) combo
(minimum number of faces:
21)

Q3Q3 / S3S3 (page
31) combo
(minimum number of vertices:
15)

T4 / gQ4P4Q4 (page
29) combo

K3 / Q3T3 (page
34) combo
(See also Szilassi
polyhedron for a further example
of the above toroid.)

Q4(T4)Q4 / B4(P4)B4 (page
39) combo
Toroids with a trucated octahedral
hull are the simplest toroids with an apolar tunnel and with a genus p>1.
The ultimate toroid in this class is K3 / 4Q3(S3) "with genus p=3 and a
minimal number of faces" [30]
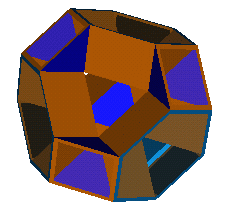
K3 / 4Q3(S3) (page 45) combo
One of Stewart's more remarkable discoveries was this drilling of the Johnson Solid: bilunabirotunda by a non-convex polyhedron he names only 'Z4'. The Z4 itself was obtained by sectioning a bilunabirotunda. The J91/Z4 combination is then used frequently in the generation of more convoluted Stewart Toroids.
Professor Stewart also explored toroids that could be formed isogonally, in the case of triangular faces, the minimal toroid proved to be this 48 faced ring of eight octahedra.
8S3 (page 51)