Chapter 10 of Professor B.M. Stewart's "Adventures Among the Toroids" (ISBN 0-686-119 36-3), focuses on toroids with a truncated cuboctahedral convex hull.
The truncated cuboctahedron (K4) can be partitioned into a central rhombicuboctahedron (E4) surrounded by six square cupolas (Q4), eight triangular cupolas (Q3) and twelve cubes (P4).
This suggests a family of
toroids of the form K4 / aQ4bQ3cP4(E4) where 0<=a<=6,
0<=b<=8 and 0<=c<=12.
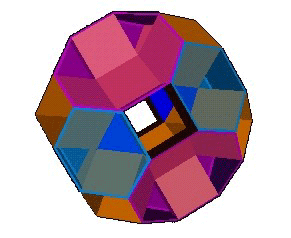
The special case of a=0, b=0, c=12 is illustrated above. This is the Stewart Toroid K4 / 12P4(E4) with genus p=11 (combo)
With a=6, b=0,
c=0
another special case is illustrated above. This is the Stewart
Toroid K4 / 6Q4(E4) with genus p=5 (combo)
The third special case is a=0, b=8, c=0 illustrated above. This is the Stewart Toroid K4 / 8Q3(E4) with genus p=7 (combo)
The above are, as have been described, special cases. Toroids exist for a number of combinations of a, b and c for a+b+c >=2. Stewart counted a total of 518 toroids of this form.
Two independent Tunnels
If we take a variation on the toroid K4 / 12P4(E4) and drill only four of the external squares, we can form a toroid of the form K4 / 4P4(E4). If we have been careful in our selection of squares for drilling we can then remove the central octagonal prism from the rhombicuboctahedron to leave the Stewart Toroid K4 / 2P4(Q4), 2P4(Q4) (combo) which has two independent tunnels. Stewart suggests that with 54 faces this seems a record low number for such a toroid.
Two storey Toroids
The central rhombicuboctahedron in the above toroids can itself be tunnelled. This gives rise to the potential for toroids of the form A / (B / C). A very attractive example is this K4 / 12P4 (E4 / Q4P4) where a rod consisting of a cuboctahedron and a cube has been re-inserted into the rhombicuboctahedral hole. This model has genus p=12.
combo1
(with the Q4P4 rod solid) - and remaining faces as frames
combo2
(with E4 / Q4P4 solid)
combo3
(with all but the K4 hull solid)