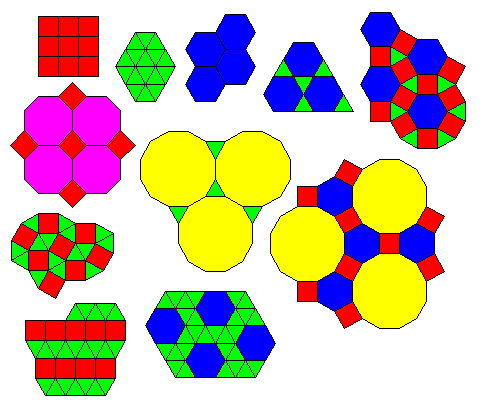
The 'traditional' eleven tessellations

There are generally held to be eleven uniform tessellations of the plane. Three regular and eight semi-regular. These tessellations are imaged above.
The three regular tessellations are:
4,4,4,4
K:E, B:-, C: 4 | 2 4 = {4,4}
3,3,3,3,3,3 K:D, B:-,
C: 6 | 2 3 = {3,6} and
6,6,6 K:F,
B:-, C: 3 | 2 6 = {6,3}
Seven of the eight semi-regular tessellations can be generated from the regular ones:
8,8,4 is a
truncated 4,4,4 K:V, B:65,
C: 2 | 4 4 = t{4,4}
4,3,4,3,3 is a snub 4,4,4 K:N,
B:66, C: | 2 4 4 = s{4 : 4}
12,12,3 is a truncated 6,6,6 K:S,
B:61, C: 2 3 | 6 = t{6,3}
6,3,6,3 is a bitruncated 3,3,3,3,3,3 or 6,6,6
K:P, B:62, C: 2 | 3 6 = {3 : 6}
6,3,3,3,3 is a snub 3,3,3,3,3,3 or 6,6,6 K:L,
B:-, C: | 2 3 6 = s{3 : 6}
6,4,3,4 is a rhombitruncated 3,3,3,3,3,3 or 6,6,6
K:Ii, B:64, C: 3 6 | 2 = r{3 : 6}
12,6,4 is a truncated 6,3,6,3 K:Mm,
B:63, C: 2 3 6 | = t{3 : 6}
only
4,4,3,3,3 cannot be generated from the regular tessellations. K:(M), B:67, C:no symbol
This quick overview is not an attempt to compete with some of the excellent primers to these tessellations available on the web, one of the nicest of which, "Totally Tessellated", is linked here.
Next: Infinite and
semi-infinite tessellations
Back: to tessellations
Home: To index