Infinite and Semi-infinite tessellations
In addition to the 'traditional' eleven tessellations of the plane. Seven further tessellations can be generated if infinite polygons (or 'apeirogons') are permitted. An apeirogon has a dihedral angle of pi and appears as a straight line.
If the apeirogons are regarded as being normal to the plane, they appear to be synonymous with the hemi-spherical polygons in uniform polyhedra.
Note: A number of these tessellations involve retrograde polygons. All apeirogons are regarded as prograde and are listed in the vertex figures as "Inf".
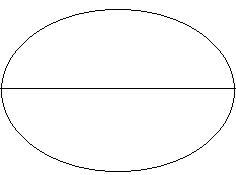
Infinite tessellation 1

Inf, Inf.
K:-, B:-, C:-
This is a trivial case of two apeirogons joined at their edges. It is actually a fourth regular tessellation. This and the next two tessellations could be regarded as families of tessellations if it is taken that an apeirogon can cycle its centre more than once, meaning there are an infinite series of apeirogons each of which could form one of these tessellations.
Infinite tessellation 2
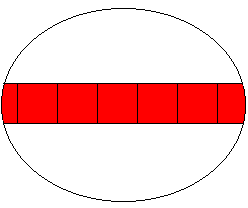
Inf, 4, 4
K:-, B:59, C: 2 oo | 2 = t{2,oo}
The apeirogons in case 1 can be separated by a band of squares to form a semi-regular tessellation. With the apeirogons normal to the plane this becomes an infinite prism.
Infinite tessellation 3
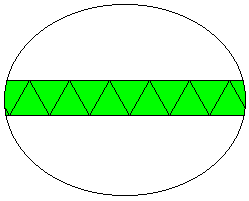
Inf, 3, 3, 3
K:-, B:60, C: | 2 2 oo = s{2 : oo}
Separating the apeirogons by a band of triangles forms another semi-regular tessellation. With the apeirogons normal to the plane this becomes an infinite anti-prism.
Infinite tessellation 4
Inf, 4, Inf, 4/3
K:E, B:-, C: 4/3 4 | oo
From this tessellation on, we start to introduce retrograde polygons. The edge/vertex network of the 4,4,4,4 tessellation forms the basis for the above semi-regular tessellation. Only the coloured squares are present.
Infinite tessellation 5
( Inf, 3, Inf, 3, Inf, 3 ) / 2
K:D, B:-, C: 3/2 | 3 oo
The edge/vertex network of the 3,3,3,3,3,3 tessellation forms the basis for the above semi-regular tessellation. Only the coloured triangles are present. This is the only tessellation to date which requires the '2' divisor as the vertex figure encircles the vertex twice.
Infinite tessellation 6
Inf, 6, Inf, 6/5
K:P, B:62, C: 6/5 6 | oo
The edge/vertex network of the 6,3,6,3 tessellation forms the basis for the above semi-regular tessellation. Only the coloured hexagons are present.
Infinite tessellation 7
Inf, 3, Inf, 3/2
K:P, B:62, C: 3/2 3 | oo
Finally the edge/vertex network of the 6,3,6,3 tessellation also forms the basis for the above semi-regular tessellation. Only the coloured triangles are present.
Apeirogons also occur in a number of the 'star' tessellations.
Next: 'Star' and
'Retrograde' Tessellations
Back:
to tessellations
Home: To index