
Rhombified Stellations of Snub Uniform Polyhedra
George Hart's 'propellohedra', (http://www.georgehart.com/propello/propello.html) introduce a form of polyhedra containing both regular polygons and kite shaped quadrilaterals.
An alternative way to form these polyhedra is to stellate a uniform snub polyhedron. A uniform snub polyhedron typically consists of m-gons, n-gons and snub triangles. If the snub triangles edge adjacent to either the {m} or {n} faces are extended such that they meet in an {m} or {n}-acral peak above the centre of the original face, then a polyhedron consisting of the remaining {n} or {m}-gonal faces and kites is the result.
These figures can be relaxed such that the kites become rhombi. George Hart discusses the icosahedral case at http://www.georgehart.com/zomebook/green-giant.html and in http://www.georgehart.com/zongker/blend-final.pdf.
A systematic search through the snub uniform polyhedra generates a number of rhombified stellations, in each case, where the vertex figure is given, the bracketed polygon is the one that has been stellated. It does appear to be the case that if the replaced polygon ({m} or {n} above) is a triangle, then the resulting kites relax into three coplanar rhombi which form a compound hexagon. The overall polyhedron which results is then similar to a uniform polyhedron:
Convex Snubs
 |
 |
Icosahedron (3)-3-3-3-3 (Snub tetratetrahedron, Tetrahedrally stellated) - 'Rhombi-propello-tetrahedron' - hexagonal faces
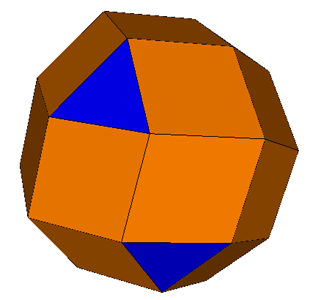
Snub Cuboctahedron (4)-3-3-3-3 'Rhombi-propello-octahedron' (above left)
Snub Cuboctahedron 4-3-(3)-3-3 'Rhombi-propello-cube' - hexagonal faces
Snub Icosidodecahedron (5)-3-3-3-3 'Rhombi-propello-icosahedron' (above right)
Snub Icosidodecahedron 5-3-(3)-3-3 'Rhombi-propello-dedecahedron'- hexagonal faces
Non-convex Snubs
 |
 |
 |
 |
Great Vertisnub Icosidodecahedron (5/3)-3-3-3-3 'Rhombi-propello-great-icosahedron ?' (above top left)
Snub Dodecadodecahedron (5/2)-3-5-3-3 (above top right)
Snub Dodecadodecahedron 5/2-3-(5)-3-3 (above bottom left)
Snub Disicosidodecahedron (5/2)-3-3-3-3-3 (above bottom right)
Snub Disicosidodecahedron 5/2-3-(3)-3-3-3 - hexagonal faces
Great Snub Icosicosidodecahedron (5/2)-3-5/3-3-3-3 - degenerate?
An omission from the above list is the Great Snub Icosidodecahedon (5/2)-3-3-3-3, as the stellated form of this figure will not relax into a rhombified form.
Other snub figures can be similarly processed to produce pseudo-hexagonal faces, but where non-triangular faces are considered they call for augmentation of the edges around a retrograde face, or around a pro-grade face where the dihedral angles involved are > 90 degrees. The adjacent edges will not meet at a point so no 'kite' faces are possible.
The anti-prisms can also be considered as snub polyhedra, and whereas all cases with n>2 can be stellated to give kite shaped faces, only in the case of n=3 can the resulting figure be relaxed into having rhombic faces, in which case the result is a cube.
Credits
I am indebted to Mason Green for suggesting that various polyhedra with kite shaped faces could be relaxed into rhombic forms.
The original stellations were produced using Great Stella and relaxed using HEDRON.