

Rhombically Expanded Deltahedra
In this page I discuss a class of polyhedra containing both rhombic and triangular faces which are face transitive within the two subsets of faces. They are formed by augmenting rhombohedra with prisms and then with pyramids, then relaxing the resulting polyhedra such that the triangles become regular and the square faces become rhombi.
Introduction
A number of deltahedra can be formed by augmenting rhombihedra. These are discussed in some detail on my deltahedra page.
For the deltahedron to be isohedral, the underlying rhombohedron must be edge transitive. The deltahedra which can be so formed are therefore restricted to those derived from the duals of the semi-regular polyhedra.
Considering first the rhombic duals, these can be augmented by rhombic prisms. This forms a set of polyhedra with a combination of square and rhombic faces. Each subset of faces is transitive. If we now augment the rhombic faces of these polyhedra with pyramids, we can form polyhedra with square and triangular faces, the triangles being distorted as they are formed from rhombic pyramids. We can however relax the figure allowing the triangles to become regular and the squares to distort into rhombi.
The resulting polyhedra contain rhombic and regular triangular faces. Face transitivity is preserved within each of the subsets. Four isomorphic figures can be formed from each of the rhombic duals, depending on whether the prisms and pyramids are augmented (outwards) or excavated (inwards) or are mixed.
The same process can be applied to the duals of the three ditrigonary uniform polyhedra, resulting in a further 12 figures.
An alternative construction of these polyhedra could involve the generation of the deltahedra as the first stage, followed by a rhombic expansion. It is notable that the degeneracy present in some of the deltahedra is resolved in these figures, none of which appear to be degenerate.
It should be stressed that the relation of the rhombic polyhedron to the original augmented polyhedron can at times be rather weak, whilst isomorphism is retained, the original polyhedron is merely the start point for a relaxation process which can itself involve significant movement.
Rhombic Duals to Uniform Polyhedra.
1. The Cube
The cube is the rhombic dual to the octahedron. This can be augmented in the same way as the remaining rhombic figures below, the process is somewhat trivial though and is for that reason excluded from further consideration.
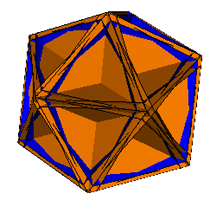
2. The Rhombic Dodecahedron
| Prisms Augmented | Prisms Excavated | |
| Pyramids Augmented |
 |
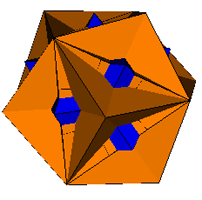 |
| Pyramids Excavated |
 |
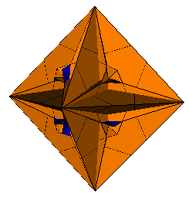 |
3. The Rhombic Triacontahedron
| Prisms Augmented | Prisms Excavated | |
| Pyramids Augmented |
 |
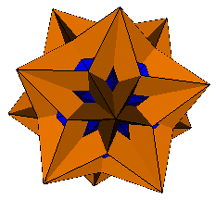 |
| Pyramids Excavated |
 |
 |
4. The Great Rhombic Triacontahedron
| Prisms Augmented | Prisms Excavated | |
| Pyramids Augmented |
 |
 |
| Pyramids Excavated |
 |
 |
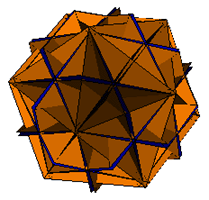
5. The Medial Rhombic Triacontahedron
| Prisms Augmented | Prisms Excavated | |
| Pyramids Augmented |
 |
 |
| Pyramids Excavated |
 |
 |
Duals to Ditrigonary Uniform Polyhedra
1. The Small Ditrigonary Icosidodecahedron


The small ditrigonary icosidodecahedron and its dual.
| Prisms Augmented | Prisms Excavated | |
| Pyramids Augmented |
 |
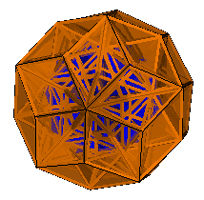 |
| Pyramids Excavated |
 |
 |
2. The Great Ditrigonary Icosidodecahedron


The great ditrigonary icosidodecahedron and its dual.
| Prisms Augmented | Prisms Excavated | |
| Pyramids Augmented |
 |
 |
| Pyramids Excavated |
 |
 |
3. The Ditrigonary Dodecadodecahedron


The ditrigonary dodecadodecahedron and its dual.
Note: the duals to the ditrigonary dodecahedron and the great ditrigonary icosidodecahedron appear similar but differ in structure with the faces of the former being uncrossed hexagons and those of the latter crossed hexagons.
| Prisms Augmented | Prisms Excavated | |
| Pyramids Augmented |
 |
 |
| Pyramids Excavated |
 |
 |
Credits
The original dual figures were produced using Great Stella and relaxed using HEDRON.