Honeycombs derived from the runcinated alternated cubic honeycomb
Two elementary honeycombs can be derived from the regular honeycomb 3RCO-P4-T (where RCO is the rhombicuboctahedron). The original honeycomb is shown below.
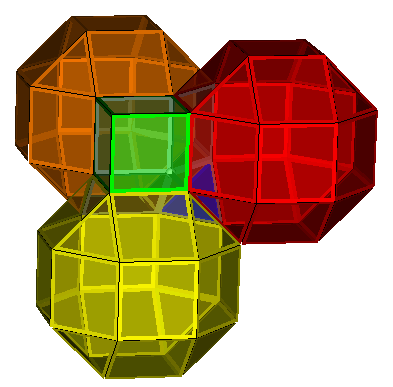
It is noticeable from the above image that there are planes passing through the vertices. These planes divide the regular honeycomb into alternate layers containing prisms and a combination of square cupolas and tetrahedra. A single vertex on the cupola/tetrahedra layer is shown below
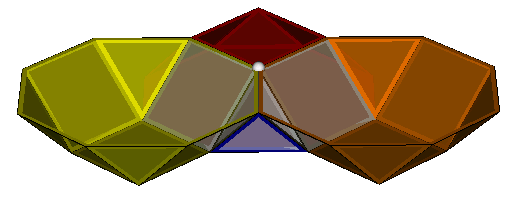
Applying the layer of prisms to this vertex gives the first elementary honeycomb, 3Q4-T-2P8-P4 shown above.
An elementary honeycomb can also be
formed by
omitting the layers of prisms and connecting the cupola/tetrahedra
layers
directly. In this case the vertex is of the form 6Q4-2T
(above).
Incidence matrices for all the above honeycombs are given by Richard Klitzing here.
Next: Honeycombs derived from the rectified cubic honeycomb (not elementary)
Back: To honeycombs index
Return: To main index