
Honeycombs derived from the rectified cubic honeycomb (not elementary)
A number of honeycombs can be derived from the regular honeycomb 4CO-2S3 (where CO is the cuboctahedron). It must be stressed that none of the honeycombs derived are elementary as the cells include triangular cupolas and octahedra, neither of which is elementary. The honeycombs are however presented below as they are related to certain of the elementary honeycombs presented on previous pages. The original honeycomb is shown below.
It is noticeable from the above image that there are planes passing through the vertices. These planes divide the regular honeycomb into layers containing triangular cupolas and octahedra. One such layer is shown below.
Stacking such layers, in the formation they appear in the original 4CO-2S3 generates the first new honeycomb, 6Q3-2S3-gyro.
If the layers are rotated with respect to each other such that the exposed octahedral faces are adjacent, then an alternate mode 6Q3-2S3-ortho can be formed. Note that the reason for naming the two honeycombs in this manner is that the above honeycomb contains the Johnson Solid 'triangular orthobicupola'.
Both of the above honeycombs can be elongated by the insertion of layers of prisms to form 3Q3-S3-2P6-2P3-gyro and 3Q3-S3-2P6-2P3-ortho respectively .
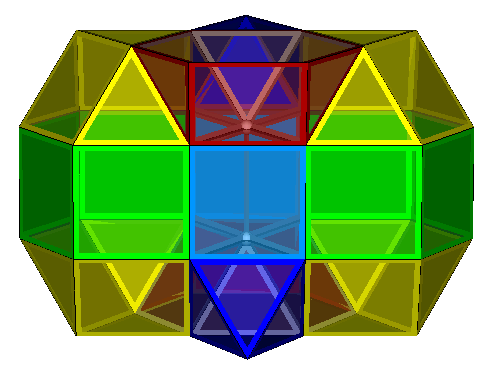
3Q3-S3-2P6-2P3-gyro |
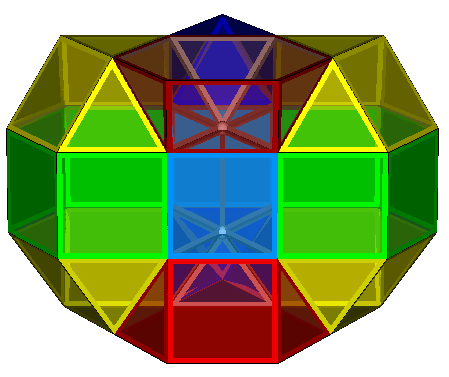
3Q3-S3-2P6-2P3-ortho |
Incidence matrices for all the above honeycombs are given by Richard Klitzing here.
Back: To honeycombs index
Return: To main index