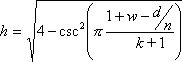
In the same way that Edge Expanded Bi-prisms can be formed from a prism of height 2, Edge Expanded Bi-Pyramids can be formed from a bi-pyramid with the apices co-incident. The insertion of a singular triangular face between each tri-angular face of the bi-pyramid forms an anti-prism of height 2. This gives the family their informal abbreviation of "EEAs". The repeated insertion of triangles gives numerous polyhedra in similar fashion to the EEBs although the number of variations seems somewhat reduced.
Note: This family is closely related to the "Accordion Polyhedra" discussed in Professor Bonnie Stewart's "Adventures Among the Toroids" 2nd Ed. pp 151. Using Professor Stewart's terminology these would be "Triangular Plated Accordions"
Using similar notation as the EEBs, the general form is the {n/d} [endo / exo] edge k-expanded w-wound bi-anti-prism where {n/d} identifies the base polygon. In short, I refer to this as an {n/d} [endo/exo] (k,w) EEA. The term 'exo' is used to denote occurences where the inserted triangles face outwards (as in the image above), 'endo' then means occurences where the inserted triangles face inwards. Making made this distinction, it actually turns out to be un-necessary as each polyhedron can be uniquely defined by a combination of k and w. For each value of k, w can at most be within limits of 0 and (k-1). However with w >= (k-1)/2 the pyramidical faces face inwards and it is easer to refer to the solid as an exo (k,w*) EEA where w* = k-w-1
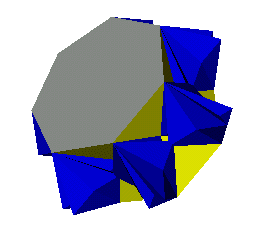
The height (h) of an {n/d} (k,w) endo EEA is given by
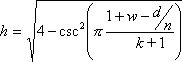
The height of the exo EEAs can be determined by using w* instead of w.
A proof of the above formula is not supplied but follows the logic given in proving the height of the EEBs.
The range of n/d > 1 for which EEA's of varying (k,w) exist is given in the following list:
(k,w)
(1,0)
n/d > 1.5 (see note below)
(2,0)
"endo (2,0)" n/d > 2
(2,1)
"exo (2,0)" all n/d
(3,0)
"endo (3,0)" n/d > 3
(3,1)
"exo (3,1)" all n/d
(3,2)
"exo (3,0)" all n/d
(4,0)
"endo (4,0)" n/d > 6
(4,1)
"endo (4,1)" all n/d
(4,2)
"exo (4,1)" all n/d
(4,3)
"exo (4,0)" all n/d
(5,0)
"endo (5,0)" does not exist
(5,1)
"endo (5,1)" n/d > 1 (n/d =
1 is the limiting case with a height of zero)
(5,2)
"exo (5,2)" all n/d
(5,3)
"exo (5,1)" all n/d
(5,4)
"exo (5,0)" all n/d
(k,w) = (1,0) is a bi-anti-prism. The limiting case of n/d = 1.5 comes from the fact that n/d < 2 generates a (2d/n) crossed-bi-antiprism. The limit of 1.5 is then equivalent to the triangular crossed bi-antiprism which has height zero.
Models have been generated where the EEA exists for n/d=7 and k<=5. As an aid to identification the original 'pyramidical' triangles are coloured yellow and the 'expanded' triangles blue. Three alternatives are presented for each mode. A 'solid' model (which tends to be dominated by the square faces in endo mode and by the triangular faces in exo mode), a 'frame' model where the base heptagons have been replaced by heptagonal frames to show the internal structure, and a 'hemi' model showing just half of the polyhedron with equatorial edges highlighted. These are probably the best option for understanding the internal structure of the polyhedron. Note the relative sparsity of 'toroid' models (as compared to the EEBs) as the heights of the exo and endo EEAs are not identical, however 'heterogenous' toroids do exist (see below).
The diagrams shown below are of the equatorial edges with the equatorial corner of the pyramidical triangle light blue and the inserted triangular edges in dark blue. The projection of the base vertices onto the equatorial plane are shown in red. Clicking on the diagrams leads to the 'hemi' models.
{7} (k/w) EEAs
{7} endo (2,0) EEA
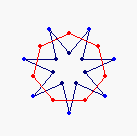
solid, frame |
{7} exo (2,0) EEA
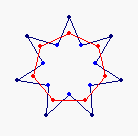
solid, frame |
{7} endo (3,0) EEA
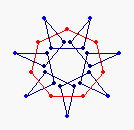
solid, frame |
{7} exo (3,0) EEA
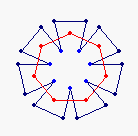
solid, frame |
| There is no endo (3,1) EEA | {7} exo (3,1) EEA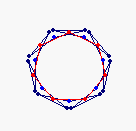
solid, frame |
{7} endo (4,0) EEA
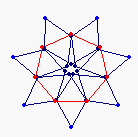
solid, frame |
{7} exo (4,0) EEA
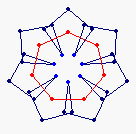
solid, frame |
{7} endo (4,1) EEA
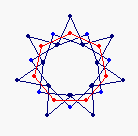
solid, frame |
{7} exo (4,1) EEA
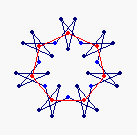
solid, frame |
| There is no endo (5,0) EEA | {7} exo (5,0) EEA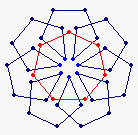
solid, frame |
{7} endo (5,1) EEA
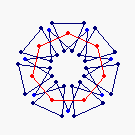
solid, frame |
{7} exo (5,1) EEA
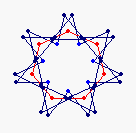
solid, frame |
| There is no endo (5,2) EEA | {7} exo (5,2) EEA

solid, frame |
It would appear from the above that the (k,w) = (4,1) case contains superposed vertices, closer examination shows that this is not the case.
Next: EEA Toroids
Back: Main