


Cupolaic Expanded Rhombohedra
In this page I discuss a class of polyhedra containing both rhombic and triangular faces which are face transitive within the two subsets of faces. They are formed by augmenting rhombohedra with rhombic cupolae and relaxing the resulting polyhedra such that the triangles become regular.
Introduction
If we consider as our base polyhedra the rhombic duals, these can be augmented by rhombic cupolae. A rhombic cupola can be thought of as a square cupola distorted such that the base face becomes a rhombus. This involves deformation of the square cupolaic faces into rhombi such that the triangular faces remain regular.
This forms a set of polyhedra with a combination of rhombic and triangular faces. Face transitivity is preserved within each of the subsets. Two isomorphic figures can be formed from each of the rhombic duals, depending on whether the cupolae are augmented (outwards) or excavated (inwards).
These models were generated by forming an approximate rhombic cupola with the required rhombic base but with distorted cupolaic faces, augmenting the base rhombic dual and then relaxing the resulting figure to give regular triangles and rhombic faces.
Rhombic Duals to Uniform Polyhedra.
1. The Cube
The cube is the rhombic dual to the octahedron. This can be augmented in the same way as the remaining rhombic figures below, the process is somewhat trivial though and is for that reason excluded from further consideration.
2. The Rhombic Dodecahedron
| Cupolae Augmented | Cupolae Excavated |
 |
 |
3. The Rhombic Triacontahedron
| Cupolae Augmented | Cupolae Excavated |
 |
 |
4. The Great Rhombic Triacontahedron
| Cupolae Augmented | Cupolae Excavated |
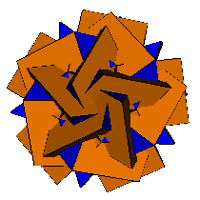 |
 |
5. The Medial Rhombic Triacontahedron
| Cupolae Augmented | Cupolae Excavated |
 |
 |
Credits
The original dual figures were produced using Great Stella and relaxed using HEDRON.
Back: To Deltahedra and Rhombihedra