
Petrie Expanded Polyhedra
Each regular polyhedron contains a set of Petrie polygons. Such polyhedra can be expanded by separation into two parts along a Petrie polygon and rejoining the parts by the insertion of rhombi. The process can then be repeated for the other Petrie polygons of the original polyhedron. Where an inserted rhombus is orthogonal to a subsequent Petrie polygon it is expanded into an irregular hexagon. The images below show the first two expansions of a dodecahedron.
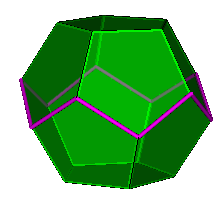 Dodecahedron with a single Petrie polygon highlighted. |
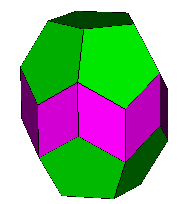 First expansion |
 Second expansion showing first irregular hexagons |
For all of the Platonic and Kepler-Poinsot polyhedra, such expansion results in a polyhedron containing the original faces of the polyhedron and a set of irregular hexagons equal in number to the number of edges in the original polyhedron.
The irregular hexagons are always convex zonogons, having the following
properties:
- planar
- all edges of equal length
- edges occur as three parallel pairs
In simple terms they can be thought of as a planar hexagonal framework in which two opposite edges have been pushed together or pulled apart allowing the two free vertices to flex outwards or inwards respectively. I refer to them in this page as 'Petrie hexagons'. Their shape can be uniquely identified by specifying the internal angle at one of the two free vertices, this I term the 'apex angle' (a). The remaining four internal angles are then 180-(a/2) degrees.
An alternate way of generating these Petrie expanded polyhedra would be to replace each edge of the original polyhedron with a hexagon and then to allow these hexagons to distort such that the free vertices coincide.
If we denote the faces, vertices and edges of the original polyhedron by (f,v,e) then the equivalent triad for the Petrie expanded polyhedron (F,V,E) is given by (f+e,v+2e,4e)
Petrie Expanded Platonic Polyhedra
 Petrie Expanded Tetrahedron (OFF) (F,V,E)=(10,16,24) a=90º |
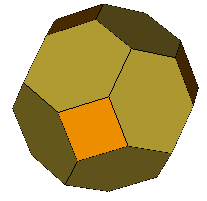 Petrie Expanded Cube (OFF) (F,V,E)=(18,32,48) a=109.471º |
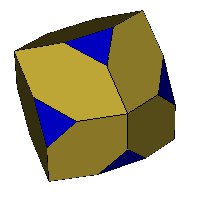 Petrie Expanded Octahedron (OFF) (F,V,E)=(20,30,48) a=70.529º |
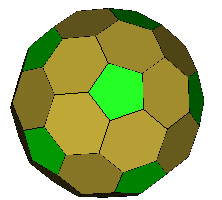 Petrie Expanded Dodecahedron (OFF) (F,V,E)=(42,80,120) a=116.565º |
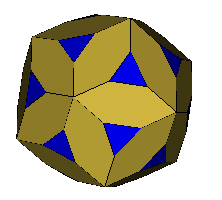 Petrie Expanded Icosahedron (OFF) (F,V,E)=(50,72,120) a=63.435º |
It is interesting to note that the apex angles of the Petrie hexagons in the dual pairs sum to 180º.
Petrie Expanded Kepler-Poinsot Polyhedra

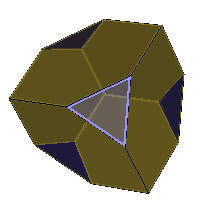
The Petrie polygons of the Kepler-Poinsot polyhedra are not as obvious, but do
exist, as can be seen in the above example of the skew decagonal Petrie Polygon in
the Great
Stellated Dodecahedron.
 Petrie Expanded Great Dodecahedron (OFF) (F,V,E)=(42,72,120) a=138.19º |
 Petrie Expanded Great Icosahedron (OFF) (F,V,E)=(50,72,120) a=116.565º |
 Petrie Expanded Great Stellated Dodecahedron (OFF) (F,V,E)=(42,72,120) a=41.81º |
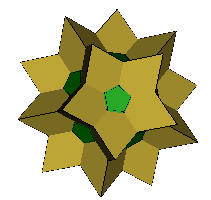 Petrie Expanded Small Stellated Dodecahedron (OFF) (F,V,E)=(42,80,120) a=63.435º |
Note that for the Petrie Expanded Great Stellated Dodecahedron the pentagonal faces are internal to the figure.
Petrie Expanded Semi-Regular Polyhedra
|
|
 Petrie Expanded Icosidodecahedron (OFF) (F,V,E)=(122,120,240) a=63.435º |
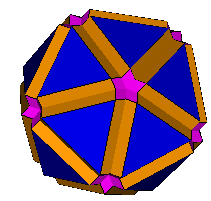 Petrie Expanded Great Icosidodecahedron (OFF) (F,V,E)=(122,120,240) a=63.435º |
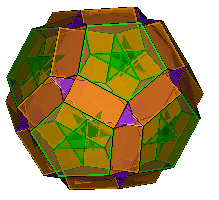 Petrie Expanded Dodecadodecahedron (OFF) (F,V,E)=(114,120,240) a=41.81º |
The Petrie polygons of the semi-regular polyhedra are planar. Expansion using these polygons results in figures containing rhombi. These are discussed in more detail here.
Credits: The polyhedra on this page were generated by a combination of Stella 4-D and HEDRON.
Next: Petrie Expanded Truncated Polyhedra
Index: Petrie Expanded Polyhedra