The Stewart G3 and its relations
A trawl through the uniform
polyhedra and the Johnson Solids
reveals that none of them contain a vertex at which a single pentagon,
square and triangle meet (a 5-4-3 'acrohedron'). So the question
has to be asked; does one exist? That answer is that one does, more
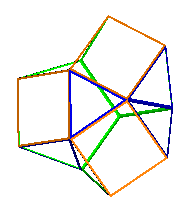
than one in fact. One of the simplest (imaged above) was originally
described by Professor Bonnie Stewart in his book "Adventures Among
the Toroids" (more on this on my Toroids
pages). Stewart names this polyhedron a 'G3', it appears
in his sectioning of a rhombicosidodecahedron.
More on the search for a '5-4-3' acrohedron and other acrohedra can be
found on my Acrohedra page.


Note the vertex of the G3
at which three pentagons meet. A dodecahedron
can be made from four such sections. So four G3s can be joined
together to form a dodecahedral shell with the squares and triangles inside.
Removing the shell leaves the above polyhedron with a tetrahedral symmetry (left
image). The right image shows the shell as a frame.

Image reproduced with permission
The image above is of a physical model
of four G3s created by Ulrich Mikloweit. His
wonderful models are unique in that he incorporates every part of each
polygonal face, including the internal facets. More images of this
polyhedron and of Ulrich's many other models can be found on his website
at http://www.polyedergarten.de

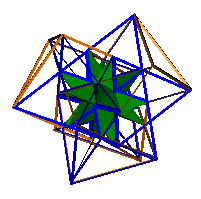
A 'great' G3 also
exists with the pentagons of the G3 replaced by pentagrams.
A vertex of the great stellated dodecahedron
now appears. Four such polyhedra can be joined to form another polyhedron
with a tetrahedral symmetry. This is shown above left, the right
image shows the internal great stellated dodecahedron.
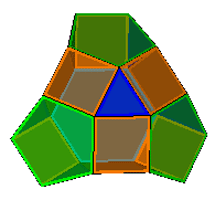

Alex
Doskey (2003) has expanded the G3 by placing square faces
between the pentagons and the triangle-triangle edges and completing the
polyhedron with triangular and hexagonal caps, the expanded
G3 is shown above left, Alex terms this a H3 (OFF). Four of these can be excavated from a rhombicosidodecahedron
to produce the figure on the right (OFF).
I am indebted to Alex Doskey
for bringing the G3
(and the whole search for a '3-4-5') to my attention.
Alex has more on this and related polyhedra at http://www.doskey.com/polyhedra/
Back: to index







