Incidence Matrices

by Dr Richard Klitzing

(reproduced with permission)

Taken purely abstract, polytopes are described by their surtopial elements plus the relative incidences. The most basic way to give those incidences are 0-1-matrices with 1 meaning "incident" and 0 "not". But already the easiest polytopes would ask for huge matrices. This is the entrance for symmetry, the symmetry of the polytope itself. Alike surtopial elements now can be classed together via symmetrical equivalence, and the incidence relation will be given for the classes instead. This reduces the size of the matrix considerably. The diagonal elements of these reduced matrices will give the total count of elements of each of the respective equivalence classes. The non-diagonal elements I_(n,m) will provide the numbers of incident surtopes of class m with any of the elements of class n. The subdiagonal parts of the rows thus still describe the surtopial element classes. The superdiagonal parts of the rows describe their environmental aspacts, i.e. vertex figures, edge figures etc.

Regular polytopes are bound to provide a single class of surtopes per dimension, but in general there will be more symmetry-inequivalent elements of the same dimensionality. Therefore it is conveniant to display the dimensional borders as well as a superimposed guiding grid. Vertex-transitivity for instance can be read off from an incidence matrix directly, as those polytopes show up only a single vertex class.

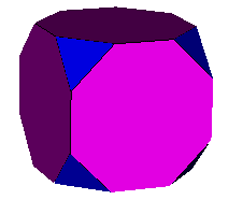
Here as an example the incidence matrix of the truncated cube is given. The Dynkin diagrams of the relative classes are provided in addition in front of the rows.

o3x4x

. . . || 24 |  2  1 | 1 2
------++----+-------+----
. x . ||  2 | 24  * | 1 1
. . x ||  2 |  * 12 | 0 2
------++----+-------+----
o3x . ||  3 |  3  0 | 8 *
. x4x ||  8 |  4  4 | * 6

This matrix shows that there are 24 vertices, all having the same symmetry (upper-left element). The lowest two rows show that the 2-dimensional elements have 3 or 8 vertices (lower-left block) and therefore are triangles or octagons. The rightmost entries of the first row show further that at each vertex 1 such triangle and 2 octagons are incident. Further there are 2 types of edges, the upper one is incident to 1 triangle and 1 octagon, the other one is incident to 2 octagons only. The middle block of the bottom two rows shows that the triangle will have all edges of the first type clearly, but the octagons do use edges of both types (alternatingly). Altogether there are 8 triangles and 6 octagons (lower-right block).

Two relations on these numbers are generally valid. The one is the equation I_(n,n)*I_(n,m)=I_(m,n)*I_(m,m). This is true whether incident representants of those classes of subpolytopes do exist or not, as in the latter case the corresponding non-diagonal elements are both zero. The other observation is, and this derives right from the diagrammatic representation of the 0-1-matrix, the so called Hasse diagram, that this diagram read top-down instead of bottom-up would describe the dual abstract polytope. The same is even true for the reduced matrices, where the matrix of the dual polytope can be read off by just rotating the matrix half way around an axis orthogonal to the writing plane, thereby interchanging counts of vertices and facets, or dualising the numbers of the vertex figures into those of facets and vice versa. Further-on to each of the subdiagonal parts of the rows, the superdiagonal parts of the rows, and the diagonal itself, the Euler formula might be applied; but appropriate extensions like genus, density etc. would have to be considered.

Note that the same polytope might be a fix-element under different symmetry groups. Thus there could be different (reduced) incidence matrices, all describing the same polytope. Especially the identity map, taken as reducing symmetry, would reproduce the 0-1-matrix. On the other hand incidence matrices just like Hasse diagrams only depend on the structure of the abstract polytope. That is, different isomorph realisations of it would have the same incidence matrix. For instance a convex polygon {n} abstractly can not be distinguished from the polygram {n/d} as long there are no incidences of different types.