Height of an Edge Expanded Bi-prism

Consider the generic{n/d} endo (k,w) EEB.

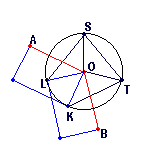
In Fig 1 below: A, O and B are successive vertices of the base polygon. K and L are equatorial vertices of the square faces. S and T are equatorial vertices of the triangular faces –

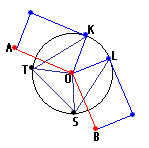
[Fig 1: Vertex diagram for endo (k,w)=(3,0)]

Angle AOB is the internal angle of the base polygon and is given by

Angles AOK and BOL are internal angles of the square faces, so:

The angle KOL is filled (i) by the base polygon plus two right angles (from the square faces) and (ii) by the angles subtended by k triangular faces meeting at O.

Let angle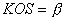 

Then angles:

i.e.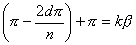

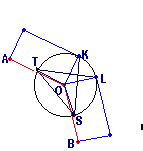
[Fig 2: Vertex diagram for endo (k,w)=(3,1)]

If the triangular faces are ‘wound’, then we need to add 2.pi.w to the left side of the above equation, where w is the ‘winding number’.
In Fig 2 above the triangular faces run counter-clockwise from K to S, then S to T and T to L.  The angle completed is from OK to OL plus 2.pi.

So: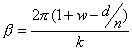 

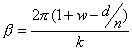
As triangles OKS, OST and OTL all have base lines in the equatorial plane then

KS = ST = TL = 1

Let distance OS = s.Then

OS = OT  = OL = s

Considering (for example) the triangle KOS, we obtain

The height (h) of the EEB is given by

So substituting for s:

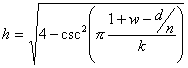
[Fig 3: Vertex diagram for exo (k,w)=(3,0)]

For exo-EEB’s, equation (A) above becomes

which simplifies again to

and so;

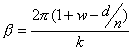
showing that the heights of the endo (k,w) and exo (k,w) EEB’s are the same.