Arruated
Polyhedra
arruated
icosahedron
(4,2)-exo
Inspired by Dr
Richard Klitzing's cuned
twisters[1, Fn 1], I have explored
further polyhedra using an icosahedron as the seed polyhedron.
One method to
generate the desired polyhedron is as follows:
1. Augment faces of
the seed polyhedron with pyramids;
2. Join
the
peaks of egde adjacent pyramids with pairs of triangles; 'wedges'
(effectively filling the valleys with distorted tetrahedra);
3. Relax
the
resulting polyhedron so that all faces are regular
triangles.[Fn 2]
The
effect is to
place one of the above wedges over each edge of the
original polyhedron.
When
George
Olshevsky first described the above process in 2006[2], he
used the term 'spheniated' [Fn 3, Fn 4]. Examples of
Olshevsky's polyhedra can be found on Roger
Kaufman's
site[3]. Mason
Green's cingulated antiprisms[4],
discovered
in
2005
turn
out
to
be
spheniated
prisms
but
Green
used
a
different
method
of
generation.
Green
found
these
by
dividing
an
n-gonal
anti-prism
into
two
equal
sections
each
containing an n-gonal prismatic cap and
its edge adjacent triangles, and inserting a 'cingulum' of 4n
triangles. They were
rediscovered in 2025 by discord user
'Harsin Sinquin' who used the approach of attaching six triangle
complexes over triangle pairs of the antiprisms, and coming up with the
term "cune". Discussion between Klitzing and Sinquin led
to the cuned twisters.
Both Olshevsky
and
Klitzing's
polyhedra only
consider applying the spheniation/cuning process to a subset of the
edges of the original
polyhedron and some of
the pyramidical faces and original faces of the seed polyhedron
remain. Because of these remaining faces, relaxation of the wedge
faces to equilateral triangles
involves a
'twist' of the remaining faces.
I
decided to explore adding pyramids and wedges to all edges. This means
all the original faces of the seed polyhedron are
augmented and the resulting pyramidical faces have been also been
replaced. This is a generalisation of 'spheniation/cuning' and as
such needed a new term. I
felt a suitable verb would be 'arruo' (to cover with earth or to
bury) hence we get the adjective 'arruated' . The
polyhedra
consist only of the faces of the
wedges. This means
that icosahedral symmetry is preserved and the 'twist' referred to
above is
replaced by the freedom to adjust the height of the pyramids to the
point where an equilibrium is obtained between the edge height of the
pyramids and the distance apart of two edge adjacent pyramids.
In
similar
fashion to the
generation of the Edge
Expanded Bi-Prisms and Bi-Antiprisms, it is possible to
insert more
than one wedge between each peak in step 2 above. I term
the group of wedges between two edge adjacent peaks a 'set'. With more than
one wedge in a set then different configurations can be obtained.
Again it is the height of the pyramids that is adjusted to obtain an
equilibrium. Solutions can also be obtained where the pyramids
have a negative
height, i.e. they are inverted.
The naming
convention is as follows:
- 'n' is
the number of wedges in each set.
- 'exo'
means
the edge angle between the (now virtual) pyramids is less than 180
degrees, 'endo' means the edge angle is reflexive.
- ''w' is
the winding
number, the number of times that the set of triangles winds around an
axis set orthogonal to to plane containing the peaks of the edge
adjacent pyramids and the origin. The direction of
winding is always outwards from the origin. High winding numbers
(> n/2) can give the appearance of being retrograde.
- The
name is then given as (n,w)-exo/endo.
In
generating the polyhedra below, I used a standard colouring format.
- If sets
consist of one or two wedges they are coloured in
yellow.
- For 3
or 4
wedges per set, the outermost ones are yellow, the inner ones
orange.
- For 5
wedges
per set the colours are as above but the central one is red.
- One set
of wedges is highlighed by having the above colours replaced with
green, cyan and blue respectively. In the VRML files linked
below, these highlighted wedges stay solid through the
'trans/frame/solid' view options.
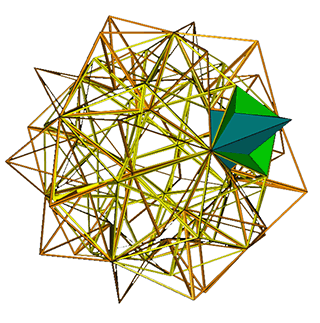
- This example has 5 wedges per
set and shown before the relaxation step.
Below,
with
notes, is a list of those generated to date with n ≤ 5. I make no claim that
the list is complete, and I would
welcome any further cases. The degenerate cases
may be specific to the seed polyhedron being the
icosahedron.
(1,0)-exo These are
equivalent to replacing
the original polyhedra with
its dual and triangulating the faces.
(1-0)-endo
The pyramids in
this case do point outwards from the base icosahedron but are so low
that the angle between them is > 180 degrees.
(2,0)-endo
(2,1)-exo
(3,0)-endo This is a
deltahedron.
All
triangular
faces
are
fully
visible.
(3,1)-endo
(3,2)-exo
(4,0)-endo
(4,1)-exo
(4,1)-endo
(4,2)-exo
(4.2)-endo
(4,3)-exo
-
this
is
degenerate,
the
four
wedges
form
faces
of
a
pentagonal
bipyramid
(with
one
open
pair)
and
then
sets
of
wedges
co-incide
in
pairs.
(5,0)-endo - this
is
degenerate, the five wedges form faces of a pentagonal
bipyramid and the inner vertices are coincident
(5,1)-exo
(5,1)-endo
(5.2)-exo
(5,3)-exo
(5,4)-exo
Other
seed
polyhedra
Numerous
polyhedra can act as the seed for this process and I will only scratch
the surface here.
Each n-goal face of the seed gets augmented with an n-gonal
pyramid, sets of wedges are then inserted as above.
(4,0)-endo
cases (coloured yellow and orange as above) are presented for the tetrahedron, octahedron (degenerate), cube and dodecahedron
(the last two are deltahedra).
As the (1,0) cases
involve the dual of the seed, I also tried starting with a dual.
These are the (4,0)-endo cases for the rhombic dodecahedron (seed) and the rhombic triacontahedron (seed) . The red
faces are
adjacent to the 4 or 5-fold
vertices, the
hidden yellow faces are adjacent to the 3-fold vertices, central wedges
are interpolated between them. Here also is an n=4
case for the rhombic enneacontahedron
(seed), wedges adjacent
to 6
fold vertices are blue, 5 fold are red and 3-fold are yellow, central
wedges are again interpolated.
With more than one type of pyramid present, the endo/exo
categorisation gets more involved and can be mixed in a single
polyhedron. Examples are linked (with no
attempt at categorisation) for the n=3
case for the icosidodecahedron
(seed), the small
rhombicosidodecahedron (seed) and the snub
icosidodecahedron (seed)
In
all
cases
the
colouring
convention
is
use the seed face for the pyramid as the colour
for adjacent wedges and to use an interpolated colour for the centre
wedge. See the links to the seed polyhedra for the case
colours.
Further combinations are possible where there is more than one edge
type to the seed polyhedron. An example was also generated (here) for the small
rhombicosidodecahedron with sets of three wedges between the pentagonal
and square pyramids, and sets of two wedges between the square and
triangular pyramids.
Credits
and
Resources
My thanks to Dr
Richard Klitzing for providing the inspiration for this page.
The
augmentation
of
the
seed
polyhedra,
creation
of
the
nets
and
initial
relaxation
was
performed
using
Great
Stella.
Stella VRML files were
then
converted into HEDRON input files using
Roger
Kaufman's VRML2OFF
utility.
Then
final
relaxation
and
VRML
generation
using
HEDRON.
A zip file containing TXT and OFF files for all polyhedra on this page
is here.
Footnotes
[Fn 1] In Latin,
the word cuneus (plural cunei), means a wedge or a
wedge-shaped object, area, or formation. This term is the source for
words like "cuneiform" (wedge-shaped writing) and "cuneus" (a
wedge-shaped part of the brain) and is a root of many English words
describing wedge-shaped forms! (Google)
[Fn 2] Relaxing a
polyhedron refers to the process of iteratively adjusting
the locations of a polyhedron's vertices such that they meet a set of
predefined criteria (e.g. all edge lengths are equal and they form
regular faces).
[Fn 3] The
prefix "spheno-" originates from the Greek word for "wedge" and refers
to something wedge-shaped or of or relating to the sphenoid bone, a
wedge-shaped bone at the base of the skull. Examples of its use include
sphenogram, meaning a wedge-shaped character, and sphenopalatine, which
refers to the sphenoid bone and the palate. (Google)
[Fn
4] Olshevsky [2]
also describes a process he terms 'ambiation'. To quote
Olshevsky:
"Ambiation
is
a
generalization
of
spheniation
to
a
patch
of
more
than
two
faces.
Specifically, the
patch is a regular n-gon surrounded on all sides by n equits
[equilateral triangles]"[2]. This process is
different from the process I am describing here.
References
1
Klitzing, R. (2025) Cuned Twisters. https://bendwavy.org/klitzing/explain/twisters.htm#cune
2.
Olshevsky
G.
(c2006) Breaking Cundy's Deltahedron record
(unpublished) linked from [3] below.
3. Kaufman R. (2008) The Cundy Deltahedra. https://www.interocitors.com/polyhedra/Deltahedra/Cundy/index.html
4. Green, M. &
McNeill J. (2005) Cingulated
Anti-prisms https://www.orchidpalms.com/polyhedra/chiral-prisms/prisms9.html
Back: to index
