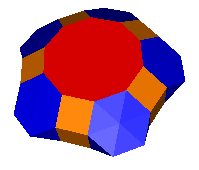
8-4-3-3 (left) and 10-4-3-3 (right)

The solutions to the 8-4-3-3 and 10-4-3-3 acrons are obviously related.  They are members of a family of polyhedra formed by wrapping a complex of squares and triangles between two polygons.   The squares are in strips of three, the triangles are in complexes of fourteen.

In addition to the above linked octagonal and decagonal models, examples can be formed for other n-gons, where n is even.    The figures continue above n=12,but as there is now an angular excess the triangular complexes become folded.

n-4-3-3 with n odd

'7'-4-3-3

Due to the alternating nature of the connecting squares and triangles, examples cannot be formed where n is odd.  However a closely related toroidal family can be generated by utilising the degenerate 2n/2-gons (such as the 14/2-gon).  Examples generated using these polygons can then have the base polygons removed leaving the edges of the square and triangular rings connected.    The resulting toroid has an n-gonal prismatic symmetry.  A number of examples are included in the zip files below.

Again, models can be generated for n/d where d>1:

'9/2'-4-3-3

Again a number of examples are included in the zip files below.

Isomerism

There are a number of distinct isomers for each n - although some appear to have limits as shown below.  The names are informal and are intended solely as an aid to recognition.  It is not known if the list below is complete.

The zip files linked below each model contain WRL, OFF and TXT files for each model in the range.  Where they can be generated, models are included for n = 5/2, 3, 7/2, 4, 9/2, 5, 11/2, 6, 7, 8, 9, 10, 11, 12, 14, 16.    
The links in the above list are zip files of each isomer for that value of n.   A large zip file containing both sets of zip files is here.
Note that in the isomer specific zip files below the star polygons have been renamed, for example, 5/2 is renamed 2d5 (2 decimal 5).  This is so the models are presented in strict sequence of increasing X.

6-433_exo   WRL  OFF n-433_exo.zip (n = 5/2 - 16)	6-433_endo   WRL  OFF n-433_endo.zip (n = 5 - 11/2)	6-433_inverted exo   WRL  OFF n-433_inverted_exo.zip (n = 5/2 - 16)
6-433 endo crossed   WRL  OFF n-433_endo_crossed.zip (n = 4 - 16)	6-433 double crown   WRL  OFF n-433_double_crown.zip (n = 4 - 16)	6-433 folded   WRL  OFF n-433_folded.zip (n = 5/2 - 14)
6-433 saucer   WRL  OFF n-433_saucer.zip (n = 5/2 - 16)	6-433 saucer2   WRL  OFF n-433_saucer2.zip (n = 5/2 - 14)	6-433 saucer3   WRL  OFF n-433_saucer3.zip (n = 5 - 16)
6-433 exo folded   WRL  OFF n-433_exo_folded.zip (n = 5/2 - 16)

6-433_chiral   WRL  OFF n-433_chiral.zip (n = 5/2 - 16)	6-433 inverted exo chiral   WRL  OFF n-433_inverted_exo_chiral.zip (n = 5/2 - 16)	6-433 chiral folded   WRL  OFF n-433_chiral_folded.zip (n = 5/2 - 12)
6-433 chiral saucer   WRL  OFF n-433_chiral_saucer.zip (n = 4 - 16)	6-433 exo chiral folded   WRL  OFF n-433_exo_chiral_folded.zip (n = 5/2 - 16)

6-433 cup   WRL  OFF n-433_cup.zip (n = 5/2 - 16) see also coplanar cases below	6-433 crowned hatbox   WRL  OFF n-433_crowned_hatbox.zip (n = 5/2 - 14)	6-433 lighthouse   WRL  OFF n-433_lighthouse.zip (n = 4 - 16)
6-433 crown   WRL  OFF n-433_crown.zip (n = 9/2 - 16)  4 is degenerate	6-433 crown2   WRL  OFF n-433_crown2.zip (n = 9/2 - 12)	6-433 crown3   WRL  OFF n-433_crown3.zip (n = 3 - 10)
6-433 hatbox   WRL  OFF n-433_hatbox.zip (n = 5/2 - 16)	6-433 crossbox   WRL  OFF n-433_crossbox.zip (n = 5/2 - 11)	6-433 crossbox2   WRL  OFF n-433_crossbox2.zip (n = 4 - 14)
6-433 eggtimer   WRL  OFF n-433_eggtimer.zip (n = 5/2 - 16)	6-433 endo cup   WRL  OFF n-433_endo_cup.zip (n = 3 - 11)

n-3-3-3-3 acrohedra.    

4-3-3-3-3

7/2-3-3-3-3

n=5/2  7/2  7/3  8/3  9/2  9/4  10/3  11/2  11/3  11/4  11/5  12/5 

Back: to acrohedra