
Near Misses based on dodecahedra
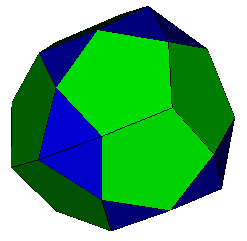
The left hand figure above with tetrahedral symmetry is termed a 'tetrated dodecahedron' by Robert Austin. It was discovered (independently) by Alex Doskey and Robert Austin. It consists of four groups of three pentagons separated by six pairs of triangles and four single triangles. With the pentagons regular, the six triangle-triangle edges are lengthened by 0.07 (stress map). Distortion (E=0.42, P=0 , A=113°).
The centre figure is a tetrahedrally expanded tetrated dodecahedron, again with the pentagons regular. (E=0.567, P=1.776, A=67.0°). Stress Map. OFF.
The right hand figure above is a 'snub expanded tetrated dodecahedron' discovered by Mick Ayrton. It can also be generated with the pentagons regular (stress map). Distortion (E=0.66, P=0 , A=88°).
I am grateful to Mick Ayrton for allowing me to display his discoveries of some near misses that have a dodecahedral origin. In all cases the distortion is confined to the triangle-triangle edges.
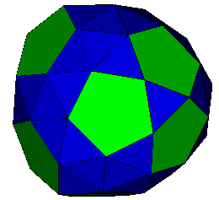
The left hand model (which Mick terms a 'saucer') contains two caps from the Johnson Solid 'trigyrate rhombicosidodecahedron'. Stress map. Distortion (E=0.214, P=0 , A=56°). Interestingly, if the pentagons are replaced by pentagonal pyramids (here), the model becomes regular. Mick has pointed out that this occurs to a surprising number of near misses.
The right hand model (which Mick terms a 'curvy octahedroid' due to the fact that it can be envisaged as having eight slightly curved compound faces) contains an interestingly twisted 'cingulum' of pentagons and triangles. Stress map. Distortion (E=0.529, P=0 , A=104°). Again this forms a regular figure if the pentagons are replaced by pentagonal pyramids (here).
The left hand model is termed a
'tripentagonal
snub dodecahedron'. The pentagons of the original dodecahedron are left in
four groups of three and snub triangles added between these groups. This
polyhedron is not convex Stress
map. Distortion (E=0.64,
P=0 , A=179°).
The right hand model is a variation on this theme, the pentagons are now left in six groups of two to form a 'bipentagonal snub dodecahedron' with a distortion of 0.646 (stress map). Distortion (E=0.64, P=0 , A=107°).
The above polyhedron was discovered by Mason Green in 2006. The distortion is confined to the triangular faces. Stress map. Distortion (E=0.570, P=0 , A=66°). It has 74 faces (6 hexagons, 12 pentagons, and 56 triangles in eight chiral clusters of seven). The hexagons and pentagons are regular, with the distortion confined to the triangles. The triangle-triangle edges are compressed by 1.78% (if adjacent to threefold axial triangles), or compressed by 0.6% (if not adjacent to axial triangles). Mason calls this the "hexagonally expanded snubbed dodecahedron"
The above polyhedron is an example of a 'fullerene', and was brought to my attention by Robert Austin and Roger Kaufman. It has tetrahedral symmetry with 12 pentagons and 4 hexagons. The above model has the distortion confined to the pentagons, stress map. Distortion (E=0.316, P=3.07 , A=52°). If the hexagons are allowed to distort (here, stress map) then the distortion becomes (E=0.059, P=2.19 , A=108°)