

Polyhedral "Twisters"
 |
 |
 |
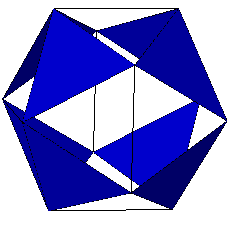
An unusual deformation of polyhedra can be constructed by taking a cuboctahedron with the square faces removed leaving eight triangular faces joined at the vertices (above left). If we allow these vertices to deform, we can twist this figure to resemble an icosahedron (above middle). A further twist collapses the figure to an octahedron (above right). This figure was first described by Buckminster Fuller, who coined it a 'Jitterbug'. A formal mathematical description of the process, and an enumeration of the Jitterbug-like set (which he terms 'dipolygonids') was completed by Dr Hugo Verheyen in his paper: "The complete set of jitterbug transformers and the analysis of their motion" a. Comp. Math. Appl., 17, Pergamon, 203-250. Oxford, 1989. b. Symmetry 2: Unifying Human Understanding, ed. I. Hargittai. Pergamon, Oxford, 1989.
I came across the simpler members of this set in "Platonic and Archimedean Solids" by Daud Sutton, published by Wooden Books Ltd in 1998 (ISBN 1-902418-34-4). The subject was also investigated independently in 1998 by Dr Richard Klitzing (summarised here) who included consideration of the regular tessellations.
My own, non-technical term for these objects is 'twisters', formal notation can be found in Verheyen.
If we consider the vertices involved, then starting with a rhombic figure having vertices of the form (a,4,b,4) we deform it into a snub figure with vertices of the form (a,3,b,3,3) and finally merge two vertices together in the final semi-regular form (a,b,a,b). In general terms I describe this process as forming an [a,b]-twister.
In addition to the three examples given in Sutton, four re-entrant twisters can be found amongst the Uniform Polyhedra. These seven are described in turn below, as is an additional case, that being a non-uniform twister which I do not believe has been previously described. (Note: this is not the complete set of dipolygonids described by Verheyen which includes more degenerate cases.) In each case, clicking on the snub image will display an animated VRML file:
Rhombic: cuboctahedron
or 'rhombic tetratetrahedron'
Snub: icosahedron or 'snub tetratetrahedron'
Semi-regular: octahedron or 'tetratetrahedron'.
Rhombic: rhombicuboctahedron
Snub: snub cuboctahedron
Semi-regular: cuboctahedron
Rhombic: rhombicosidodecahedron
Snub: snub icosidodecahedron
Semi-regular: icosidodecahedron
Rhombic: rhombidodecadodecahedron
Snub: snub dodecadodecahedron
Semi-regular: dodecadodecahedron
The rotation of the [5/2,5]-twister can be continued to form the following:
Rhombic: complex
rhombicosidodecahedron (degenerate)
Snub: vertisnub dodecadodecahedron
Semi-regular: dodecadodecahedron
Rhombic: small
complex rhombicosidodecahedron (degenerate)
Snub: great snub icosidodecahedron
Semi-regular: great icosidodecahedron
The rotation of the [5/2,3]-twister can be continued to form the following:
Rhombic: great
rhombicosidodecahedron
Snub: great
vertisnub icosidodecahedron
Semi-regular: great icosidodecahedron
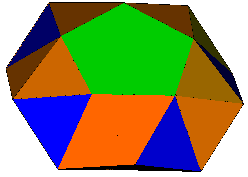
As well as the figures given above, an infinite family of dihedral twisters exists where the vertices are not uniform. This family connects the antiprisms, snub anti-prisms and gyrobicupolas. The latter of these sets a limit for this family of n/d < 6. The examples below show members of this family for values of n/d at 5, 5/2 and 7/3. For values of n/d with d even, the gyrobicupola is degenerate. Clicking on the images of the snubs below leads to VRMLs of the twisters.
 |
 |
 |
| Rhombic: pentagonal
gyrobicupola Snub: pentagonal snub antiprism Semi-regular: pentagonal antiprism |
Rhombic: pentagrammic
gyrobicupola (degenerate) Snub: pentagrammic snub antiprism Semi-regular: pentagrammic antiprism |
Rhombic: heptagrammic
gyrobicupola Snub: heptagrammic snub antiprism Semi-regular: heptagrammic antiprism |
These twisters also exist for 3/2 < n/d < 2. The crossed anti-prism setting the lower bound. Cases have been generated for n/d = 5/3 and 7/4.