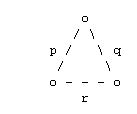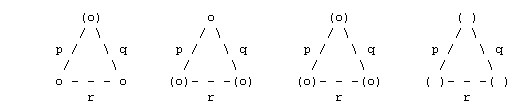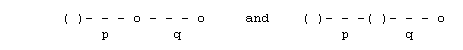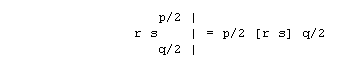Wythoff Symbols and TOCID Symbols

Contents
1. Wythoff Symbols 
2. Wythoff Symbols (modified notation)
3. TOCID notation
4. Table of Platonic and Archimedian Solids
5. Table of Uniform Star Polyhedra 
6. Blends of Polyhedra

I am indebted to Dr Norman Johnson for providing this explanation of Wythoff Symbols and TOCID symbols, and for giving me permission to include his work here. JM. 

1. Wythoff Symbols

A Schwarz triangle is a spherical, Euclidean, or hyperbolic triangle that covers S^2, E^2, or H^2 a finite number of times when repeatedly reflected in its sides. In Wythoff's construction the vertices of a uniform polyhedron or tessellation are the kaleidoscopic images (or half the images) of a suitably chosen point on the boundary or in the interior of some Schwarz triangle. A Schwarz triangle (p q r), with angles pi/p, pi/q, pi/r, may be represented by the Coxeter diagram below:


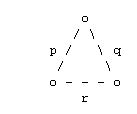
The polyhedron or tessellation is represented by its Wythoff diagram, in which one or more nodes of the Coxeter diagram are ringed. For a snub figure all three nodes are ringed and then the nodes are removed.

In their 1954 monograph "Uniform Polyhedra", Coxeter, Longuet-Higgins and Miller employed Wythoff's construction systematically to obtain all the uniform polyhedra that can be realized in Euclidean space, as well as a number of uniform tessellations of the Euclidean plane. In doing so they identified each polyhedron or tessellation by a Wythoff symbol based on the associated Schwarz triangle (p q r), indicating which nodes in the Wythoff diagram are ringed or that the diagram has three nodeless rings. Their symbols generally take one of the forms

Certain polyhedra or tessellations are "blends" of two other figures and have symbols with four numbers.

The four Wythoff symbols above correspond to the Wythoff diagrams

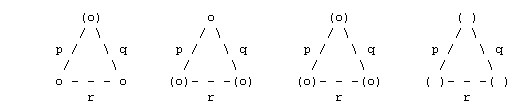
2. Wythoff Symbols (modified notation)

There is also an improved version of the Wythoff symbol that is somewhat more intuitive and that has several other advantages. In the modified notation, the corresponding Wythoff symbols are

   
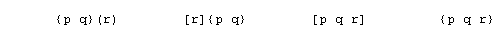
In general, the face polygons of the respective uniform polyhedra are {p}'s and {q}'s; {p}'s, {q}'s, and {2r}'s; {2p}'s, {2q}'s, and {2r}'s; and {p}'s, {q}'s, and {r}'s surrounded by triangles. However, a "digon" {2} is merely an edge.

Two other possible Wythoff diagrams are


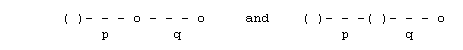
with p even in the first case and q even in the second. The respective Wythoff symbols are


The face polygons of the first figure are {p/2}'s and {q}'s. Those of the second are {p}'s, {q/2}'s, and triangles. Again, any {2}'s may be ignored.

Polyhedra or tessellations (usually nonorientable) obtained as blends of other figures having the same vertices and edges and some of the same faces include the "versi-quasi-regular" figures


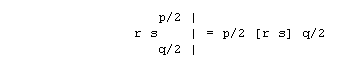
The four numbers in the symbol indicate that the figure is derived from >two< Schwarz triangles, (r s p/2) and (r s q/2). The face polygons are {2r}'s and {2s}'s.

The unique uniform polyhedron with eight faces at a vertex ("Miller's monster") has the symbol

| 3/2 5/3 3 5/2 = {3/2 5/3 3 5/2}.

Its face polygons are {3}'s, {5/2}'s, and squares, with the faces of each type occurring in coplanar pairs.

Among the advantages of the modified notation are that it is easy to see what kind of faces a figure has and to recognize figures that are closely related or that belong to the same class. Moreover, unlike the original notation, the modified Wythoff symbols are readily extended to
uniform polychora or 3-honeycombs obtained by Wythoff's construction from Goursat tetrahedra.

3. TOCID Notation

Wythoff symbols are natural companions to the TOCID notation whereby each Platonic or Archimedean solid is denoted by a symbol based on its Keplerian name. From the octahedron O = {2 3}(4) or the cube C = {2 4}(3) we can derive the quasi-regular cuboctahedron CO = {3 4}(2), and from the icosahedron I = {2 3}(5) or the dodecahedron D = {2 5}(3) we can derive the analogous icosidodecahedron ID = {3 5}(2). The "tetratetrahedron" TT = {3 3}(2) is the same as the octahedron. Other uniform solids can be obtained from the regular and quasi-regular solids by means of one of the operations of "rectification," "simiation," or "tomiation," denoted by prefixing one of the lower-case letters 'r', 's', or 't'. In keeping with Kepler's terminology, 'r', 's', and 't' can also be rendered as "rhomb(i)-," "snub," and "truncated."

The TOCID notation can be extended to the Kepler-Poinsot polyhedra and other uniform star polyhedra, as well as to prisms, antiprisms, and crossed antiprisms. In the symbol for a quasi-quasi-regular or versi-quasi-regular polyhedron, one or two lower-case letters indicate the kind and number of faces such a polyhedron has in addition to (or instead of) the faces found in the associated quasi-regular polyhedron. Originally, no distinction was made between octagons and octagrams or between decagons and decagrams. But a slight modification of the notation makes it possible to specify each type of face uniquely.

The letters 'a', 'b', 'c', 'd', 'e', 'i', and 'r' may be regarded as nominal abbreviations for certain descriptors, corresponding to a given number of faces, as follows:

a     4 hexagons
b     6 octagons
c     6 octagrams
d     12 decagons
e     12 decagrams
i     20 hexagons
r     N squares (N=6, 12 or 30) 

Below I list all the uniform polyhedra, convex or starry, with their TOCID symbols, Wythoff symbols, and names. In a few cases polyhedra can be derived in more than one way and so have alternative symbols and names. Such duplications are indicated by giving the canonical TOCID symbol in parentheses after the alternative name.

4. The Platonic and Archimedean Solids

5. Uniform Star Polyhedra

6. Blends of polyhedra

In the list below I have grouped sets of three polyhedra with the same
vertices and edges, each being a "blend" of the other two.