
Augmenting the great snub icosidodecahedron
The great snub icosidodecahedron, vertex figure (5/3,3,5/2,3,3,3)
This polyhedron offers a number of interesting augmentations. The 5/3 face can be excavated by a prism or an antiprism. The 5/2 face can be excavated by a 5/3 cupola. Combinations of these can occur. Prisms can be augmented with pyramids or with 5/3 cupola . Cupolas can be augmented with pyramids . The diagram below is an attempt to summarise the augmentations found to date:
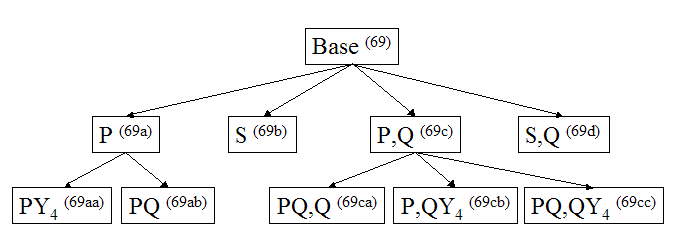
The notation above refers first to the polyhedron excavating the 5/3 face (mandatory) and after the comma, the polyhedron excavating the 5/2 face (optional). Where a polyhedron is subsequently augmented or excavated, a second letter is added.
P refers to an excavation by a 5/2
prism,
S to an excavation by a 5/2 antiprism,
Q to an excavation by a 5/3 cupola ,
Y4 to an augmentation by a square
pyramid.
PY4 is a 5/2
prism with square faces augmented by square
pyramids (solid, frame)
PQ is a 5/2
prism with one cap excavated by a 5/3 cupola
(solid, frame)
QY4 is a 5/3 cupola
with square faces augmented by square pyramids
(solid, frame)
Colour coding in all subsequent models is as follows:
5/2 and 5/3 face of great snub icosidodecahedron: light green
3 face of great snub icosidodecahedron: blue5/2 face of 5/2 prism: dark green
4 face of 5/2 prism: orange
3 face of square pyramid augmented to 5/2 prism: orange4 face of 5/3 cupola: yellow
3 face of 5/3 cupola: cyan
10/3 face of 5/3 cupola: red
3 face of square pyramid augmented to 5/3 cupola: yellow5/2 face of 5/2 antiprism: dark green
3 face of 5/2 antiprism: pink
Left (P 69a): Each retrograde pentagrammic face of the great snub icosidodecahedron can be excavated with a pentagrammic prism completing a cycle around the axis. This has the effect of uncrossing the original vertex figure. The 5/3 in the vertex figure is replaced by (4,4) The original vertex figure becomes (4,4,3,5/2,3,3,3)/2 with new vertices of (5/2,4,4). All vertices are on the exterior of the polyhedron.
Centre (PY4 69aa): Each square face of the pentagrammic pyramids in the above polyhedron (69a) be further augmented with a square pyramid. Each 4 in the vertex figure is replaced by a (3,3). The original vertex figure becomes (3,3,3,3,3,5/2,3,3,3)/2. The (5/2,4,4) vertices in the first augmentation become (5/2,3,3,3,3) vertices. New vertices are of the form (3,3,3,3). The figure is dominated by the square pyramids. The original vertices remain just visible. All vertices are on the exterior of the figure. Unfortunately I have not yet been able to generate a VRML model of this polyhedron, but clicking on the image above will show a larger image.
Right (PQ 69ab): Alternatively, the cap of each of the pentagrammic pyramids in the above polyhedron (69a) can be further augmented with a 5/3-cupola. The cupolas themselves are not locally convex but the act of joining them to the pentagrammic caps removes the retrograde polygon. The original vertices of (4,4,3,5/2,3,3,3)/2 are unaffected. The 5/2 in the (5/2,4,4) vertices is replaced by (4,3,4)/2 to give (4,3,4,4,4)/2 vertices. New vertices are added of the form (10/3,3,4). All vertices are on the exterior of the polyhedron.
Left (S 69b): Another augmentation of the original great snub icosidodecahedron can be obtained by excavating each retrograde pentagrammic face with a pentagrammic antiprism which cycles the axis. This has the effect of uncrossing the original vertex figure. The 5/3 in the vertex figure is replaced by (3,3,3) The original vertex figure becomes (3,3,3,3,5/2,3,3,3)/2 with new vertices of (5/2,3,3,3). All vertices are on the exterior of the polyhedron.
Right (S,Q 69d) : Each retrograde pentagrammic face of the great snub icosidodecahedron can be excavated with a pentagrammic anti-prism completing a cycle around the axis. Each prograde pentagrammic face of the great snub icosidodecahedron is then excavated with a 5/3-cupola. The cupolas themselves are not locally convex but the act of joining them to the pentagrammic caps removes the retrograde polygon. The overall effect is to uncross the original vertex figure. The 5/3 in the vertex figure is replaced by (3,3,3) and the 5/2 is replaced by (4,3,4)/2 The original vertex figure becomes (3,3,3,3,4,3,4,3,3,3)/3 with new vertices of (5/2,3,3,3) from the antiprisms and (10/3,3,4) from the cupolas. All vertices are on the exterior of the polyhedron.
Left (P,Q 69c) : Each retrograde pentagrammic face of the great snub icosidodecahedron can be excavated with a pentagrammic prism completing a cycle around the axis. Each prograde pentagrammic face of the great snub icosidodecahedron is then excavated with a 5/3-cupola. The cupolas themselves are not locally convex but the act of joining them to the pentagrammic caps removes the retrograde polygon. The overall effect is to uncross the original vertex figure. The 5/3 in the vertex figure is replaced by (4,4) and the 5/2 is replaced by (4,3,4)/2 The original vertex figure becomes (4,4,3,4,3,4,3,3,3)/3 with new vertices of (5/2,4,4) from the prisms and (10/3,3,4) from the cupolas. All vertices are on the exterior of the polyhedron.
Right (PQ,Q 69ca) : A second order augmentation can again be formed from the previous polyhedron (69c) by excavating the pentagrammic prismatic caps with 5/3-cupolas. The original vertices of (4,4,3,4,3,4,3,3,3)/3 are unaffected. The 5/2 in the (5/2,4,4) vertices is replaced by (4,3,4)/2 to give (4,3,4,4,4)/2 vertices. A second set of (10/3,3,4) vertices are added. All vertices are on the exterior of the polyhedron.
Left (P,QY4 69cb) : Another second order augmentation can again be formed from the previous polyhedron (69c) by augmenting the square faces of the 5/3-cupolas with square pyramids. The 4's originating from the cupolas in the original vertices of (4,4,3,4,3,4,3,3,3)/3 are replaced by (3,3) to give vertices of (4,4,3,3,3,3,3,3,3,3,3)/3. The (5/2,4,4) vertices are unaffected. The 4 in the (10/3,3,4) vertices is again replaced by (3,3) to give vertices of the form (10/3,3,3,3). New vertices are added of the form (3,3,3,3). All vertices are on the exterior of the polyhedron.
Right (PQ,QY4 69cc) : In a combination of the previous two operations, the square faces of the 5/3-cupolas can be excavated with square pyramids and the pentagrammic prismatic caps with 5/3-cupolas. The 4's originating from the cupolas in the original vertices of (4,4,3,4,3,4,3,3,3)/3 are replaced by (3,3) to give vertices of (4,4,3,3,3,3,3,3,3,3,3)/3. The 5/2 in the (5/2,4,4) vertices is replaced by (4,3,4)/2 to give (4,3,4,4,4)/2 vertices. The 4 in the (10/3,3,4) vertices from the original set of 5/3 cupolas is replaced by (3,3) to give vertices of the form (10/3,3,3,3). New vertices are added of the form (3,3,3,3). A new set of (10/3,3,4) vertices is added. All vertices are on the exterior of the polyhedron.
Note: the following further combinations did not lead to
valid augmentations:
PY4Q PY4,Q P,QY3
SQ S,QY4 S,QY3