Hyperbolic Star Tessellations
Starred tessellations also exist on the Hyperbolic plane. Regular, semi-regular and uniform tessellations can all be generated.
An excellent introduction to the Hyperbolic Plane and beautiful images of regular (non-starred) tessellations has been generated by Don Hatch (one of the co-authors of Tyler) - it is linked here. See also Hironori Sakamoto's World of Uniform Tessellations.
Regular Star Tessellations
(click on the image for a larger version)
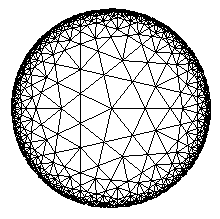
The above image shows a {7/2, 7} tessellaton. The notation {p,q} meaning that q p-gons are arranged around each vertex. A regular tessellation of the form {p/2, p} exists for all p>=7 where p is odd. It may not be easy to see the pattern of 7/2-gons from the above image, in which case a second image is presented here which has one vertex and its surrounding 7/2-gons highlighted. Note that as the dual of a {p,q} is a {q,p} then tessellations also exist of the form {p, p/2} i.e. p p-gons wrapped twice around each vertex - the grid for the {p, p/2} is the same as that for {3, p} - e.g. this {3,7} contains {7, 7/2}..
For p>=8 and p even, p/2 does not generate a star polygon, however if p/2 is regarded as two 'p/2'-gons with one gyrated by 2*pi/p with regard to their common centre, (think of a 6/2-gon as a Star of David - examples of 6/2, 8/2 and 10/2), then a family of 'pseudo'-regular tessellations can be generated, for example this {8/2, 8}
Interestingly, the form {p/2, p} also extends for n<7. For n=6, {6/2,6} is a uniform (planar) tessellation of 6/2-gons results (this example has one vertex highlighted). {5/2,5} is a small stellated dodecahedron. {4/2,4} is not a polyhedron as a 4/2-gon in this sense is a pair of crossed line segments. {3/2,3} is equivalent to {3,3} the tetrahedron (although in {3/2,3} all the triangles are retrograde.
Semi-regular Star Tessellations
(click on the image for a larger version)
The above image shows a tessellation with a vertex figure of 7/2, 3, 7/2, 3, 7/2, 3. It is one of an infinite number of such figures.
Other examples of such tessellations are:
7/2, 7, 7/2, 7
7/3, 7, 7/3, 7, 7/3,
7
7/2, 4, 7/2, 4,
7/2, 4, 7/2, 4
and to show that not all such tessellations have
to have heptagons:
5/2, 4, 5/2, 4,
5/2, 4, 5/2, 4
Uniform Star Tessellations
(click on the image for a larger version)
The above image shows a tessellation with a vertex figure of 4, 7/3, 4, inf. It is formed by taking a {7, 3} tessellation and replacing the heptagons with 7/3-gons sized such that their edges can be joined by squares.
Thanks again to Melinda Green and Don Hatch's Tyler applet which was used to generate all of these images.