The snub anti-prisms are convex for n-gonal bases up to an n of 4.744567331.. The 19/4 snub anti prism (n=4.75) is very close to this limit. This is difficult to see on the full shape as it involves four revolutions of the snub faces around the base 19/4-gon. Click here for a cut-away showing only one revolution of the snub faces. Interestingly, despite the departure from coplanarity being only 0.1 degrees, this is visible on the VRML model.

The proof follows:

Position the prism with O at the origin and with a prismatic base in the XY plane.

R is the centre of revolution and is placed on the X-axis.

S, O and S' are vertices of the prismatic base.

L, M and N are snub vertices.

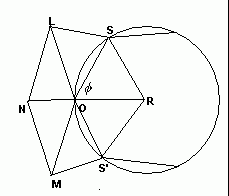
Co-ordinates of R are ( r, 0, 0)

Co-ordinates of S are ( c, s, 0)

As OR = SR this gives r = 1/2c

Let co-ordinates of L be ( -x ,y, -z)

Co-ordinates of N are ( 2x, 0, -2z)

As triangles LNO and MNO are coplanar then

or

Distance LO = 1 so

Distance LS = 1 so

Solving the above gives

As L and M are identical snub vertices then they are the same distance from the axis of revolution

So LR = NR (ignoring the z component)

i.e. the distance ( -x, y) to ( r, 0) is equal to the distance ( -2x, 0) to ( r, 0)

Equating the two gives the quadratic

Which solves to give

 The vertex and the central angle of a polygon are related by the formula:

where theta is half of the central angle. (Proof is here)

Turning back to the prismatic face, the general n-gon has the sum of its central angles given by

So in full

Which numerically is n = 4.74456733125464..