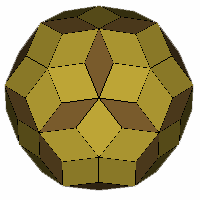
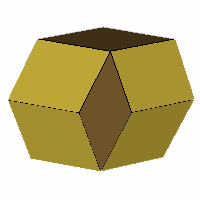
The Rhombic Enneacontahedron and relations
The above 90 sided figure is the rhombic enneacontahedron. It consists
of sixty fat rhombi ('R') (gold coloured) as found in the rhombic dodecahedron and thirty
thin rhombi ('r') (bronze coloured) as found in the medial rhombic
triacontahedron. It is a zonohedron, and is
also referred to as a zonohedrified dodecahedron. It can only be formed
from these particular rhombi, a quality I refer to as being rhombo-static.
The centre figure is a rhombo-flexible
triacontahedron.
There is a isomorph to the rhombic
enneacontahedron: the great rhombic enneacontahedron,
shown above right.
Partial zonohedrifications of the
dodecahedron
As a zonohedron bands of parallel edges can be removed from the polyhedron
leaving a remnant polyhedron which is also normally rhombo-static, although
there are some exceptions.
To define partial zonohedrifications of the
dodecahedron it is useful to label the 10 axes of the dodecahedron as A through
J. As an axis of the dodecahedron is equivalent to two opposite faces of
an icosahedron, these axes are best shown on an icosahedron as follows:
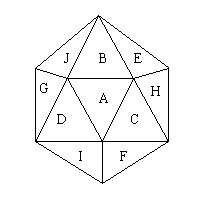
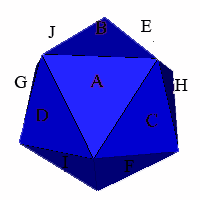 .
.
In total there are 210 possible
combinations of axes. Any selection of just one axis leads to a line
segment. There are two distinct ways to select two axes, those relating to
edge connected triangles (eg AB) and those related to vertex connected triangles
(eg BC).
These selections lead to a thin ('r') rhombus and a fat ('R') rhombus
respectively. For three or more axes the figures are given
below. All possible selections of axes are equivalent to one of the
selections below as is shown in tabular form here.
The selected axes are shown on the icosahedron
next to each figure, note that in most cases this icosahedron has been rotated
to show the symmetry of the polyhedron. Note also that all cases including
those where the symmetry is given as 'none' are symmetric through central
inversion.
In 1970 Steve Baer described a dissection of the
rhombic enneacontahedron into 120 parallelepiped blocks [1]
. The blocks are in five forms, denoted
A B C D
and E
(my italics). These are
equivalent to the 3 axes cases below. The
reference to Baer gives the number of Baer Cells required to construct the
polyhedron in the form (A,B,C,D,E).
The data was generated by David Koski and
is included here with his permission. George
Hart has an interesting page on dissections
of rhombohedra which includes discussion of the rhombic enneacontahedron.
David Koski
has also discovered the interesting facts that hold true for all the polyhedra
below:
If axes = n then:
- Surface Faces = (n)*(n-1)
- Total Faces = (n)*(n-1)*(n-2)
- Ratio of surface faces to total faces = 1/(n-2)
10 Axes
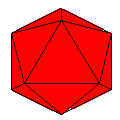
Axes: ABCDEFGHIJ
Symmetry: icosahedral
Rhombi: (R,r) = (60,30)
Baer: (10,20,30,30,30) |
VRML, OFF
|
|
9 Axes

Axes: ABCDEFGHI
Symmetry: 3-fold dihedral
Rhombi: (R,r) = (48,24)
Compliment: A
Baer: (7,14,21,21,21) |

VRML, OFF
|
|
8 Axes

Axes: ABCDEFGH
Symmetry: 2-fold pyramidical
Rhombi: (R,r) = (38,18)
Compliment: BC
Baer: (5,10,14,13,14) |

VRML, OFF
|
|
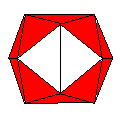
Axes: ABCDEFHI
Symmetry: 2-fold dihedral
Rhombi: (R,r) = (36,20)
Compliment: AB
Baer: (4,8,14,16,14) |

VRML, OFF
|
|
7 Axes
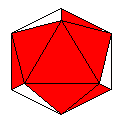
Axes: ABCDEFG
Symmetry: 3-fold pyramidical
Rhombi: (R,r) = (30,12)
Compliment: CDE
Baer: (4,7,9,6,9) |

VRML, OFF
|
|
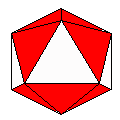
Axes: ABCDEFH
Symmetry: 2-fold pyramidical
Rhombi: (R,r) = (28,14)
Compliment: ADE
Baer: (3,6,9,9,8) |

VRML, OFF
|
|
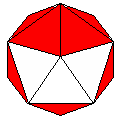
Axes: ABCDEGH
Symmetry: 2-fold pyramidical
Rhombi: (R,r) = (26,16)
Compliment: ABC
Baer: (2,4,9,11,9) |

VRML, OFF
|
|
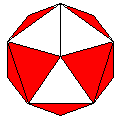
Axes: ABCDFGH
Symmetry: 2-fold pyramidical
Rhombi: (R,r) = (28,14)
Compliment: ACE
Baer: (3,6,8,9,9) |

VRML, OFF
|
|
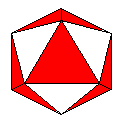
Axes: ABDEFGH
Symmetry: 3-fold dihedral
Rhombi: (R,r) = (30,12)
Compliment: BCD
Baer: (3,8,9,6,9) |

VRML, OFF
|
|
|
6 Axes

Axes: ABCDEF
Symmetry: None*
Rhombi: (R,r) = (20,10)
Compliment: ACDE
Baer: (2,3,5,5,5) |

VRML, OFF
|
|
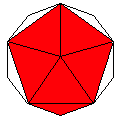
Axes: ABCDEH
Symmetry: 2-fold pyramidical
Rhombi: (R,r) = (18,12)
Compliment: ABDE
Baer: (1,2,6,7,4) |
VRML, OFF
|
|
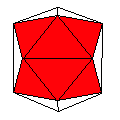
Axes: ABCDFH
Symmetry: 2-fold dihedral
Rhombi: (R,r) = (20,10)
Compliment: BCEF
Baer: (2,4,4,6,4) |

VRML, OFF
|
|

Axes: ABCDGH
Symmetry: 2-fold pyramidical
Rhombi: (R,r) = (18,12)
Compliment: ABCE
Baer: (1,2,4,7,6) |

VRML, OFF
|
|

Axes: ABCEFG
Symmetry: None*
Rhombi: (R,r) = (22,8)
Compliment: BCDE
Baer: (2,5,5,3,5) |

VRML, OFF
|
|

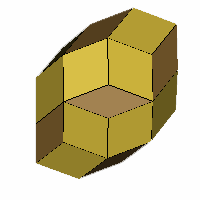
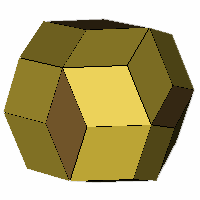
Axes: BCDEFG
Symmetry: Tetrahedral
Rhombi: (R,r) = (24,6)
Compliment: AEFG
Baer: (4,4,6,0,6)
Rhombo-flexible |
VRML, OFF
|
|
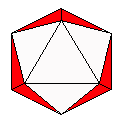
Axes: ABDEGH
Symmetry: 3-fold dihedral
Rhombi: (R,r) = (18,12)
Compliment: ABCD
Baer: (0,2,6,6,6) |

VRML, OFF
|
|
|
5 Axes
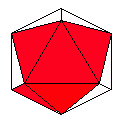
Axes: ABCDE
Symmetry: None*
Rhombi: (R,r) = (12,8)
Compliment: ABCEF
Baer: (1,1,2,4,2) |
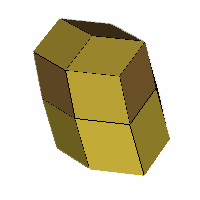
VRML, OFF
|
|
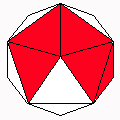
Axes: ABCEF
Symmetry: None*
Rhombi: (R,r) = (12,8)
Compliment: ABCDE
Baer: (0,1,3,3,3) |
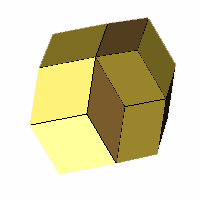
VRML, OFF
|
|
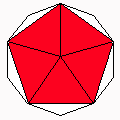
Axes: ABCEH
Symmetry: 5-fold dihedral
Rhombi: (R,r) = (10,10)
Compliment: ACDGH
Baer: (0,0,5,5,0) |

VRML, OFF
|
|
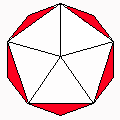
Axes: ACDGH
Symmetry: 5-fold dihedral
Rhombi: (R,r) = (10,10)
Compliment: ACDEF
Baer: (0,0,0,5,5) |
VRML, OFF
|
|
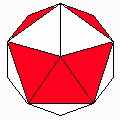
Axes: ABEFG
Symmetry: 2-fold pyramidical
Rhombi: (R,r) = (16,4)
Compliment: BCDEF
Baer: (1,4,2,1,2) |

VRML, OFF
|
|
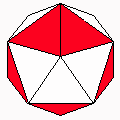
Axes: BCDEF
Symmetry: 2-fold pyramidical
Rhombi: (R,r) = (16,4)
Compliment: ABDEF
Baer: (2,2,3,0,3)
Rhombo-flexible |

VRML, OFF
|
|
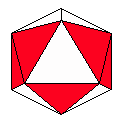
Axes: ABDEF
Symmetry: 2-fold pyramidical
Rhombi: (R,r) = (14,6)
Compliment: ABDEF
Baer: (1,2,2,2,3) |

VRML, OFF
|
|
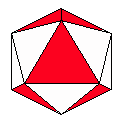
Axes: ACDEF
Symmetry: 2-fold pyramidical
Rhombi: (R,r) = (14,6)
Compliment: ABEFG
Baer: (1,2,3,2,2) |

VRML, OFF
|
|
4 Axes
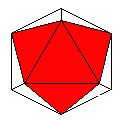
Axes: ABCD
Symmetry: 3-fold dihedral
Rhombi: (R,r) = (6,6)
Compliment: ABDEGH
Baer: (1,0,0,3,0) |

VRML, OFF
|
|
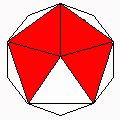
Axes: ABCE
Symmetry: 2-fold pyramidical
Rhombi: (R,r) = (6,6)
Compliment: ABCDGH
Baer: (0,0,2,2,0) |

VRML, OFF
|
|
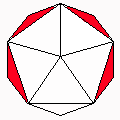
Axes: ABDE
Symmetry: 2-fold pyramidical
Rhombi: (R,r) = (6,6)
Compliment: ABCDEH
Baer: (0,0,0,2,2) |

VRML, OFF
|
|
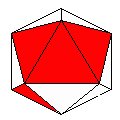
Axes: ACDE
Symmetry: None*
Rhombi: (R,r) = (8,4)
Compliment: ABCDEF
Baer: (0,1,1,1,1) |

VRML, OFF
|
|

Axes: AEFG
Symmetry: Octahedral
Rhombi: (R,r) = (12,0)
Compliment: BCDEFG
Baer: (0,4,0,0,0) |

VRML, OFF
|
|
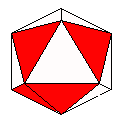
Axes: BCDE
Symmetry: None*
Rhombi: (R,r) = (10,2)
Compliment: ABCEFG
Baer: (1,1,1,0,1) |
VRML, OFF
|
|
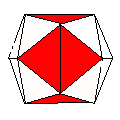
Axes: BCEF
Symmetry: 2-fold dihedral
Rhombi: (R,r) = (8,4)
Compliment: ABCDFH
Baer: (0,0,2,0,2) |
VRML, OFF
|
|
|
3 Axes
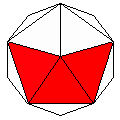
Axes: ABC
Symmetry: 2-fold pyramidical
Rhombi: (R,r) = (2,4)
Compliment: ABCDEGH
Baer: 'D'
(0,0,0,1,0)
|

VRML, OFF
|
|
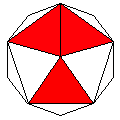
Axes: ACE
Symmetry: 2-fold pyramidical
Rhombi: (R,r) = (4,2)
Compliment: ABCDFGH
Baer: 'C'
(0,0,1,0,0) |
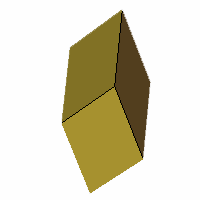
VRML, OFF
|
|
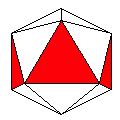
Axes: ADE
Symmetry: 2-fold pyramidical
Rhombi: (R,r) = (4,2)
Compliment: ABCDEFH
Baer: 'E' (0,0,0,0,1) |
VRML, OFF
|
|
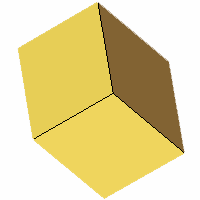
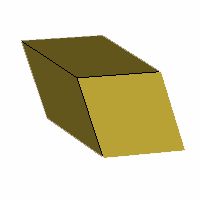
Axes: BCD
Symmetry: 3-fold dihedral
Rhombi: (R,r) = (6,0)
Compliment: ABDEFGH
Baer: 'A'
(1,0,0,0,0) |
VRML, OFF
|
|
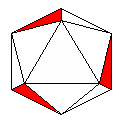
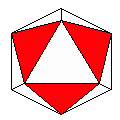
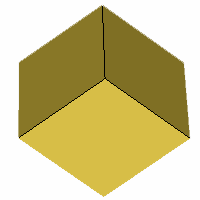
Axes: CDE
Symmetry: 3-fold dihedral
Rhombi: (R,r) = (6,0)
Compliment: ABCDEFG
Baer: 'B'
(0,1,0,0,0) |
VRML, OFF
|
|
|
Rhombo-flexible cases.
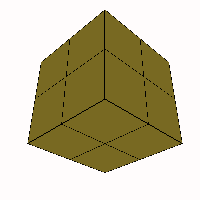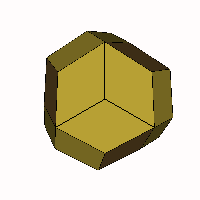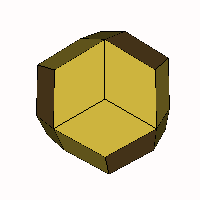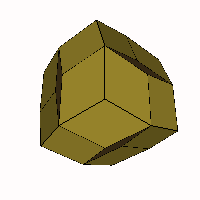
For cases with more than 4 axes only two cases
are rhombo-flexible:
- The 6-axis case BCDEFG
(above) is rhombo-flexible, and is convex between limiting cases of R and r having acute
angles of 90° and 0° (a frequency two cube) and 60° and 90° (a
truncated octahedron) with the rhombic triacontahedron as an intermediate
form.
- The 5-axis case BCDEF
is also rhombo-flexible between the same limits with the rhombic
icosahedron as an intermediate form. The animated VRML is linked here.
All 4-axis and 3-axis cases are rhombo-flexible.
Credits
My thanks to David Koski for providing
information relating to Baer Cell construction and for his permission to
republish his data.
References
[1] Baer, Steve, Zome Primer,
Zomeworks, 1970.





