

| R | 3 | 4 | 5 | 6 | 8 | 10 |
| 30 | - | - | - | - | - | - |
| R | 3 | 4 | 5 | 6 | 8 | 10 |
| 20 | - | - | - | - | - | - |
| R | 3 | 4 | 5 | 6 | 8 | 10 |
| 12 | - | - | - | - | - | - |
Convex Polyhedra containing Golden Rhombi
The Rhombic Triacontahedron ('RTC') is the dual to the icosidodecahedron. It is formed from 30 identical rhombic faces. These faces have an acute angle of arc-tan(2) or 63.435 degrees. They are sometimes referred to as 'golden rhombi'.
A number of polyhedra can be formed containing such rhombi. They can be simply divided into two categories:
I endeavour to list on this page all known polyhedra which meet the following criteria:
Index: 13 polyhedra in total
Rhombic Triacontahedron and family: 3 polyhedra
Expanded Rhombic Triacontahedron and family: 6
polyhedra
Decagonal Square Barrel and family: 4 polyhedra
Credits
Related pages
1. Rhombic Triacontahedron and related polyhedra
 |
 |
 |
||||||||||||||||||||||||||||||||||||||||||
| 1.1 RTC (VRML, OFF) | 1.2 Reduced RTC (VRML, OFF) | 1.3 Twice Reduced RTC (VRML, OFF) | ||||||||||||||||||||||||||||||||||||||||||
|
|
|
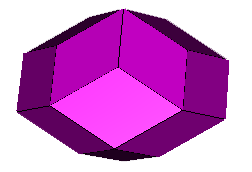
Commentary: The Rhombic Triacontahedron ('RTC') contains a number of 'bands' where all edges are parallel (RTC with one highlighted band). One such band can be removed and the remaining two parts of the RTC moved together to form a convex polyhedron with 20 faces, this can be termed a 'Reduced RTC' (it is perhaps more commonly known as the 'Rhombic Icosahedron'). The process can be repeated by the removal of a band from the reduced RTC (reduced RTC with one highlighted band) to give a 12 faced polyhedron, the 'Twice Reduced RTC' (also known as 'Bilinski's Rhombic Dodecahedron' or the 'Second Form of the Rhombic Dodecahedron'). This also contains bands, but the resulting hexahedral 'Three Times Reduced RTC' (two forms: A and B) are rhombo-flexible.
2. Expanded RTC ('XRTC') and related polyhedra
 |
 |
 |
||||||||||||||||||||||||||||||||||||||||||
| 2.1 XRTC (VRML, OFF) | 2.3 Twice reduced XRTC (VRML, OFF) | |||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||
 |
 |
 |
||||||||||||||||||||||||||||||||||||||||||
| 2.4 Three times reduced XRTC ('skinny version') (VRML, OFF) | 2.5 Three times reduced XRTC ('fat version') (VRML, OFF) | 2.6 Four times reduced XRTC (VRML, OFF) | ||||||||||||||||||||||||||||||||||||||||||
|
|
|
Commentary: The Expanded Rhombic Triacontahedron ('XRTC') can be produced from the Rhombic Triacontahedron by a process of expansion. Each face of the Rhombic Triacontahedron is moved outwards until there is a distance of one unit between each originally adjacent face. These gaps are filled by the insertion of square faces. The remaining holes, corresponding to the original vertices of the Rhombic Triacontahedron can be filled by triangles and pentagons.
The XRTC contains a total of six 'bands' where all edges are parallel (XRTC with one highlighted band). One such band can be removed and the remaining two parts of the XRTC moved together to form a new convex polyhedron, this is termed a 'Reduced XRTC'. This polyhedron now contains 5 bands each of which is equivalent (reduced XRTC with one highlighted band). The process of reduction can be repeated by the removal of a band from the reduced XRTC to give a 'Twice Reduced XRTC'. This polyhedron now contains 4 bands which fall into 2 sets of 2 bands (twice reduced XRTC with two highlighted bands). Removal of a band from one set results in a 'Three Times Reduced XRTC form A' whilst removal of a band from the other set results in a 'Three Times Reduced XRTC form B'. Both of these forms contain 3 bands which within each form are equivalent (three times reduced XRTC form A with one highlighted band, three times reduced XRTC form B with one highlighted band). Removal of one band from either form results in a 'Four Times Reduced XRTC'. This contains two bands, but the removal of either band results in the Johnson Solid 'elongated pentagonal gyrobirotunda (J43)' which contains no rhombi.
George Hart discusses these figures on his page 'Zonish Polyhedra'. George however, constructs them in a different way, starting with the icosidodecahedron and adding 'zones'. George has also produced sculptures of the Three times reduced XRTCs, see his page: 'Fat and Skinny'.
3. Decagonal Square Barrel and related polyhedra
 |
||||||||||||||||||||||||||||||||||||||||||||
| 3.1 Decagonal Square Barrel (VRML, OFF) | ||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||
 |
 |
 |
||||||||||||||||||||||||||||||||||||||||||
| 3.2 Decagonal Square Barrel plus pentagonal cupola (VRML, OFF) | 3.3 Decagonal Square Barrel plus two pentagonal cupolas (ortho) (VRML, OFF) | 3.4 Decagonal Square Barrel plus two pentagonal cupolas (gyro) (VRML, OFF) | ||||||||||||||||||||||||||||||||||||||||||
|
|
|
Commentary: The decagonal square barrel was discovered by Roger Kaufman and is one of an infinite family of polyhedra containing rhombic faces. Only the decagonal form contains golden rhombi. (See also the hexagonal square barrel). The decagonal square barrel can have one or both of its decagonal faces augmented with a pentagonal cupola. Despite appearances, it cannot be augmented with a pentagonal rotunda as the edge adjacent triangular faces become coplanar.
Roger Kaufman: Decagonal Square Barrel and the terms 'rhombo-static' and 'rhombo-flexible'.
George
Hart: 'Zonish
Polyhedra'
Convex Polyhedra containing Rhombi as found
in the
Rhombic Dodecahedron
120� rhombi: Alex
Doskey's: Diamond
Regular Polyhedra
and Steve
Waterman's: Convex
Hulls having Regular Diamonds
Robert Tupelo-Schneck's: Convex
regular-faced polyhedra with conditional edges
108� rhombi: Roger Kaufman's: 108 Degree Rhombohedra
Back: to
Deltahedra
and Rhombohedra
Back:
to Index