Petrie Expanded Truncated Polyhedra

The set of Archimedean Polyhedra contains five members formed by truncating the Platonic polyhedra.  These polyhedra contain truncated Petrie Polygons where edges of the Petrie Polygon of the Platonic polyhedron are alternated with added edges orthogonal to the symmetry axis of the Petrie Polygon.  

Petrie Expanded Truncated Platonic Polyhedra

Petrie Expanding the truncated Platonic Polyhedra results in a set of figures where the faces of the original Platonic polyhedron are separated by 'Petrie Hexagons' and the edges between an original Platonic face and a face generated by the original truncation are separated by squares.  The 'Petrie Hexagons' in each case have the same angles as those formed by the Petrie Expansion of the Platonic Polyhedra.

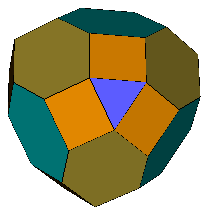
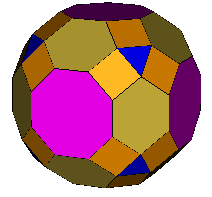
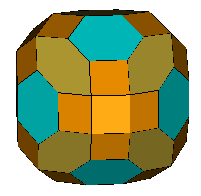
Petrie Expanded Truncated Tetrahedron (OFF) (F,V,E)=(26,36,60) a=90º	Petrie Expanded Truncated Cube (OFF)  (F,V,E)=(50,72,120) a=109.471º	Petrie Expanded Truncated Octahedron (OFF) (F,V,E)=(50,72,120) a=70.529º
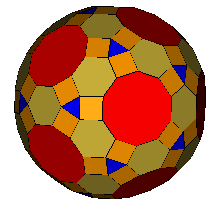
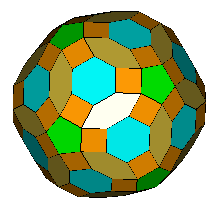
Petrie Expanded Truncated Dodecahedron (OFF) (F,V,E)=(122,180,300) a=116.565º	Petrie Expanded Truncated Icosahedron (OFF) (F,V,E)=(122,180,300) a=63.435º

Petrie Expanded Truncated Kepler-Poinsot Polyhedra

Petrie Expanded Great Truncated Dodecahedron (OFF) (F,V,E)=(122,180,300) a=63.435º	Petrie Expanded Great Truncated Icosahedron (OFF)  (F,V,E)=(122,180,300) a=116.565º
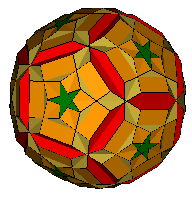
Petrie Expanded Great Stellated Truncated Dodecahedron (OFF) (F,V,E)=(114,180,300) a=138.19º	Petrie Expanded Small Stellated Truncated Dodecahedron (OFF) (F,V,E)=(114,180,300) a=41.81º

Other Petrie Expanded Truncated Polyhedra

Next: Skew Polygon Expanded Polyhedra

Index: Petrie Expanded Polyhedra