
Great Icosidodecahedron ?
An unexpected isomer to the great icosidodecahedron. (Isomer: solid model, frame). I believe this isomer is the 'great' equivalent to the isomer to the icosidodecahedron where the two "rotundas" are blended by reflecting one of them through the equatorial decagon (Isomer: solid model, frame).
A 'blend' of antiprisms.
This polyhedron is made up of two 5/2-anti-prisms (red and green) and two 5/2 crossed anti-prisms (orange and yellow) arranged as follows: a 5/2-anti-prism is placed next to a 5/2 crossed anti-prism such that one pentagrammic face of each coincide. This process is repeated with the other two constituents to form a second similar solid. This is placed over the original solid such that the two open ends of each solid coincide and the open end of the 5/2 crossed anti-prism of the second solid is coincident with the open end of the 5/2-anti-prism of the first. It has the unusual property that all vertices are of the form {3,6}. This polyhedron was first described by Dr Richard Klitzing who has since generated this 7/3-gonal equivalent. Such blends are possible for all n/d-gonal anti-prisms with 2 < n/d < 3
Mason Green's website includes a topologically regular 8/3 variant.
Self augmented heptagonal antiprism
This polyhedron (VRML, OFF) is formed by taking a heptagonal antiprism and augmenting it (inwards) with seven further heptagonal antiprisms. This process can be performed with any antiprism but the heptagonal result is perhaps the most attractive. The faceted {7/3} heptagrammic faces and the faceted triangular faces imply that faceted forms of this polyhedron may exist, however it can be shown that there are none. Further interesting heptagonal polyhedra can be found by performing the same process with a {7/2}-cupola.
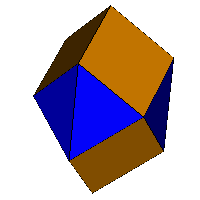
The Edshammar Polyhedron (11E) |
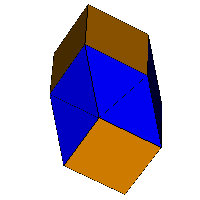
14E |
The above left polyhedron has been known to crystallographers since its description by Edshammar in 1969 [1]. It has six square and six triangular faces and 11 vertices (VRML, OFF). It is space filling, connecting triangles forms layers that can then be stacked (sample layer: VRML, OFF). It can be considered as the convex hull of two interpenetrating cubes with exactly three coincident vertices [2].
It is a near miss polyhedron, deformation (E=0.464, P=0, A=126.3°) with all deformation confined to the triangle-triangle edges which are stretched by some 15%. Stress map.
The Edshammar figure is referred to as 11E in [2]. This paper also discusses further figures (generalized Edshammar polyhedra) such as 14E (above right) (VRML, OFF) and other figures of the form 5+3nE with n>=1. 8E is the cube. All figures with n>=4 contain coplanar triangles. All members of the family are space-fillers with members up to 17E occurring naturally. 14E has deformation (E=0.569, P=0, A=126.3°). Stress map. Note how the square faces are in different alignments between members of the form 5+3nE where n is odd (such as 11E) and those where n is even (such as 14E).
If the square faces in the above polyhedra are allowed to distort into rhombi, then the triangular faces can be made regular. In all cases (excluding the cube), the rhombi have an acute angle of 82.819°. Rhombified 11E: VRML, OFF. Rhombified 14E: VRML, OFF.
References and credit.
[1] L.-E. Edshammar, 'X-Ray Studies on Binary Alloys of Aluminium with Platinum Metals', Dissertation, University of Stockholm 1969.
[2] Sven Lidin,* Thomas Popp, Mehmet Somer,and Hans Georg von Schnering Angew. 'Generalized Edshammar Polyhedra for the Description of a Family of Solid-state Structures', Agnew. Chem. Int. Ed. Engl. 1992, 31, No. 7 pp 924-927
I am grateful to Wolfhang Hornfeck for bringing this family of polyhedra to my attention.
The above polyhedron is the 'associahedron'. The name derives from the fact that there are 14 ways to bracket 5 numbers. Each vertex of the associahedron corresponds to one particular bracketing. An edge exists between two vertices if the two bracketing patterns that correspond to these two vertices differ by only one set of brackets - labelled version. More information can be found at: http://www.cs.bsu.edu/homepages/fischer/math215/associahedron.html
The association cannot be made with
regular faces, in the above image all faces are distorted (Stress
map) Distortion:
(E=0.097,
P=2.779, A=47.9°). If we confine the
distortion to the pentagons only then the 'A' value increases to
224.8° as the
square faces become
highly distorted.
Thanks to Roger Kaufman for bring
this near miss to my attention and to Mark Spindler for pointing me to
the modified distortion option.