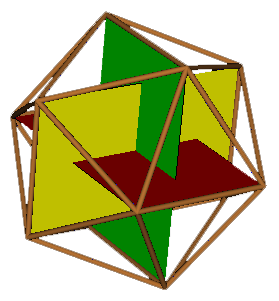
Phi in the icosahedron and dodecahedron

The golden ratio (phi) is defined as (sqrt(5)+1) / 2 and is approximately equal to 1.618...

Phi occurs repeatedly in the construction of the icosahedron and dodecahedron.  A simple example shows how phi occurs in the co-ordinates of these polyhedra

The twelve vertices of the icosahedron can all be defined by placing three orthogonal rectangles with side ratio phi:1 at the origin.  If we define t = phi/2, the resulting co-ordinates are then
(�t,  ��, 0), (��, 0, �t) and (0, �t,  ��).

The vertices of the dodecahedron can be formed in a similar fashion, in this case place three orthogonal rectangles with side ratio phi�:1 at the origin.  if we define u=phi�/2, the resulting twelve co-ordinates are then (�u,  ��, 0), (��, 0, �u) and (0, �u,  ��). The remaining eight vertices can then the formed by placing a cube of side length phi at the origin with its faces parallel to the planes of the rectangles.  With t = phi/2 as before, the resulting co-ordinates are then (�t,  �t, �t).

I am indebted to Daud Saum's book 'Polyhedra' [ref] for bringing these relationships to my attention.